Lern-Archiv [3]: Mathematik

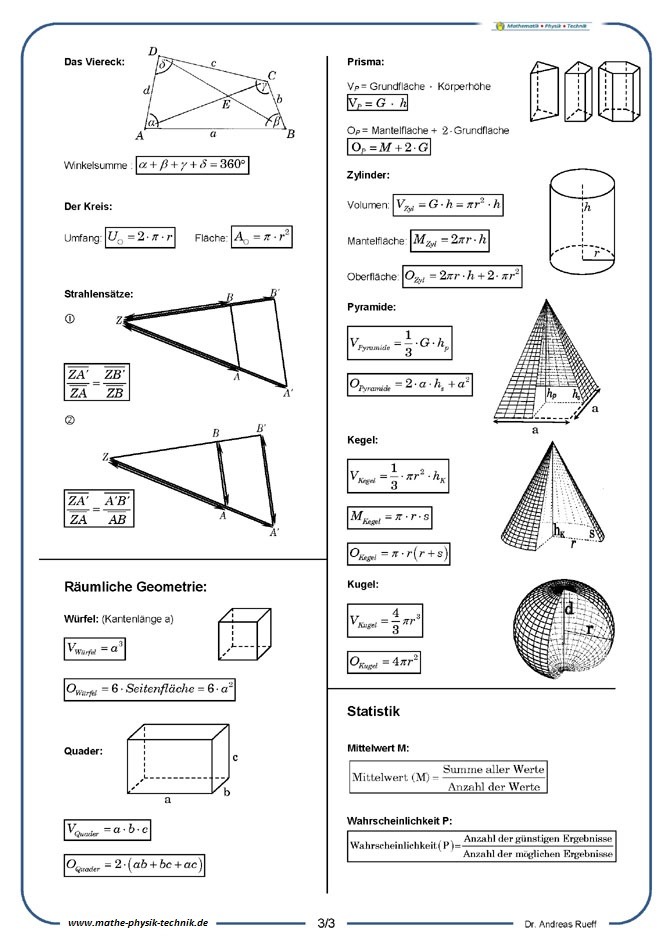
Geometrie - Kegel - Die Oberfläche [8:13]
Oberflächenformel für den Kreiskegel
Die Formel zur Berechnung der Oberfläche eines Kegels wird anschaulich hergeleitet. Anschließend werden die Ergebnisse zusammengefasst und ein Beispiel vorgerechnet.
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Geometrie - Kegel - Volumenformel [4:45]
Volumenformel für den Kreiskegel
Herleitung der Volumenformel für den Kreiskegel, ausgegangen wird hier von der Volumenformel der Pyramide. Anschließend wird noch ein Beispiel vorgerechnet.
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Geometrie - Kugel - Oberfläche [4:06]
Herleitung der Oberflächenformel für eine Kugel
Anschaulich gezeigt wird die Herleitung der Oberflächenformel für die Kugel.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Geometrie - Kugel - Volumen [3:55]
Herleitung der Volumenformel für eine Kugel.
Dabei wird auf das experimentelle Differenzverfahren für unregelmäßige Körper und den Volumen von Kegel und Zylinder aufgebaut.
(Das Video zeigt nicht die ausführliche mathematische Herleitung.)
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

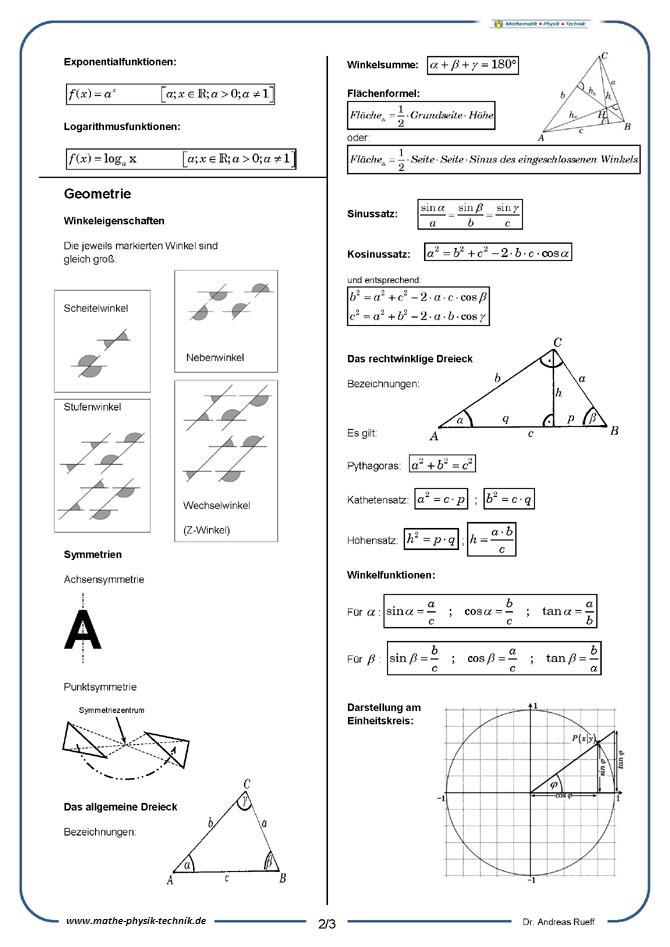
Geometrie: Der Sinussatz [5:03]
Herleitung des Sinussatzes
Der Sinussatz - Anschaulich beschrieben wird die Herleitung des Sinussatzes. Damit lassen sich Winkel und Seiten eines allgemeinen Dreiecks berechnen.
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Geometrie: Der Kosinussatz [4:50]
Herleitung des Kosinussatzes
Berechnungen in Dreiecken: Die Herleitung des Kosinussatzes als grundlegenden Zusammenhang der Trigonometrie und Grundlage zur Berechnung von Seiten und Winkeln in Dreiecken wird anschaulich dargestellt.
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Einstiegsvideos in die Analysis (Kl. 11) zur Wiederholung der benötigten Grundlagen sind:
siehe auch: Themenseite - Analysis
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)



Analysis: Folgen und Reihen - Gaußsche Summenformel:
Analysis - Veranschaulichung der Summenformel [3:58]
Die Gaußsche Summenformel wird anhand eines Beispiels erklärt und anschließend verallgemeinert.
siehe auch: Themenseite - Analysis
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analysis: Exponentialfunktionen ableiten (1): [6:36]
Graphisches Ableitungsverfahren
Mathematik - Analysis: Es wird die Ableitung von Exponentialfunktionen am Beispiel von f(x)=2^x graphisch vorgeführt. Im zweiten Teil wird das rechnerische Differenzieren (mit Differentialquotient) gezeigt.
siehe auch: Themenseite - Analysis
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analysis: Exponentialfunktionen ableiten (2): [3:23]
Rechnerisches Ableitungsverfahren
Mathematik - Analysis: Es wird die Ableitung von Exponentialfunktionen am Beispiel von f(x)=2^x rechnerisch vorgeführt. Im ersten Teil wird das graphische Ableitungsverfahren zu dieser Funktion gezeigt.
siehe auch: Themenseite - Analysis
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analysis: Integralrechnung (1): [12:26]
Obersumme, Untersumme, Flächeninhaltsfunktion
Es werden die Grundgedanken der Integralrechnung mit Obersumme, Untersumme und Flächeninhaltsfunktion erklärt. Eingeleitet wird über eine geometrische Frage zur Volumenberechnung. Zwei einfache Beispiele führen anschließend zur allgemeinen Regel für Flächeninhaltsfunktionen.
siehe auch: Themenseite - Analysis
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analysis: Integralrechnung (2): [7:36]
Stammfunktion, Integral, Hauptsatz
Gezeigt wird der Zusammenhang zwischen Flächeninhaltsfunktion und Stammfunktion. Dies führt zum Hauptsatz der Differnetial- & Integralrechnung (unbestimmtes und bestimmtest Integral). Ein Beispiel demonstriert abschließend die Anwendung.
siehe auch: Themenseite - Analysis
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (1): [4:53]
Punkte im Raum - Entfernungen im Raum (1)
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Beschrieben wir die Darstellung von Punkten im Raum (R^3). Anschaulich dargestellt wird die Entfernungsformel eines Punktes vom Ursprung.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (2): [5:03]
Punkte im Raum - Entfernungen im Raum (2)
Beschrieben wir die Darstellung von Punkten im Raum (R^3). Anschaulich dargestellt wird die Entfernungsformel für die Berechnung der gegenseitigen Entfernung von zwei Punkten.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (3): [6:29]
Vektoren: Spaltenvektor - Ortsvektor - Betrag eines Vektors
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Beschrieben wir die Darstellung von Vektoren im Raum (R^3). Anschaulich dargestellt wird die mathematische Beschreibung von Vektoren in der Schreibweise als Spaltenvektoren. Die Begriffe "Ortsvektor" und "Betrag" werden an Beispielen eingeführt.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (4): [4:01]
Vektoren: Addition und Subtraktion
Beschrieben und anschaulich dargestellt wird die Addition und subtraktion von Vektoren im Raum (R^3).
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (5): [3:33]
Vektoren: Skalar-Multiplikation
Beschrieben wird die Multiplikation von Vektoren. Hierbei wird die erste Variante (Skalar-Multiplikation) gezeigt und veranschaulicht.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (6): [4:21]
Vektoren: Skalarprodukt (1) - linear abhängige Vektoren
Beschrieben wird die Multiplikation von Vektoren. Hierbei wird die zweite Variante (Skalarprodukt) zunächst für linear abhängige Vektoren gezeigt und veranschaulicht.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (7): [5:26]
Vektoren: Skalarprodukt (2) - linear unabhängige Vektoren
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Beschrieben wird die Multiplikation von Vektoren. Hierbei wird die zweite Variante (Skalarprodukt) für linear unabhängige Vektoren gezeigt und veranschaulicht.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (8): [5:47]
Vektoren: Vektorprodukt (Kreuzprodukt)
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Beschrieben wird die Multiplikation von Vektoren. Hierbei wird die dritte Variante (Vektorprodukt/Kreuzprodukt) anhand eines Beispiels berechnet und veranschaulicht.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (9): [7:14]
Geraden im Raum: Geradengleichungen
Beschrieben und anschaulich dargestellt wird die Darstellung von Geraden im Raum. (Parameterform und Zweipunkteform der Gerade)
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (9b): [5:10]
Untersuchung der Lagebeziehung Punkt/Gerade
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Beschrieben und anschaulich dargestellt wird die Untersuchung der Lage eines Punktes zu einer Geraden im Raum. Beide Möglichkeiten werden rechnerisch demonstriert.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (10): [5:47]
Ebenen im Raum (1): Ebenengleichungen
Beschrieben und anschaulich dargestellt wird die Darstellung von Ebenen im Raum. (Parameterform und Dreipunkteform der Ebene)
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (11): [6:42]
Ebenen im Raum (2): Ebenengleichungen (Normalengleichung)
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Beschrieben und anschaulich dargestellt wird im zweiten Teil zu den Ebenengleichungen die Darstellung von Ebenen im Raum durch die Normalform der Ebenengleichung.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (12): [7:17]
Ebenen im Raum (3): Koordinatengleichung und Achsenbschnittsform der Ebene
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Beschrieben und anschaulich dargestellt an einem Beispiel wird im dritten Teil zu den Ebenengleichungen die Darstellung von Ebenen im Raum durch die Koordiantenform der Ebenengleichung. Als Spezialfall wird die Achsenabschnittsform ebenfalls veranschaulicht.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (12b): [6:08]
Lagebeziehungen: Ebene und Punkt
Beschrieben und anschaulich demonstriert werden die möglichen Lagebeziehungen eines Punktes zu einer Ebene. Die rechnerische Untersuchung wird an einem Beispiel vorgeführt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (12c): [6:54]
Lagebeziehungen: Ebene und Gerade mit Schnittpunktsberechnung
Beschrieben und anschaulich demonstriert werden die möglichen Lagebeziehungen einer Gerade zu einer Ebene. Die rechnerische Untersuchung des Schnittpunktes wird an einem Beispiel vorgeführt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (13): [5:29]
Aus zwei Ebenen (Parameterform und Normalenform) wird die Schnittgerade berechnet und veranschaulicht.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
siehe auch: Themenseite - Analytische Geometrie



Analytische Geometrie (14): [4:49]
Aus zwei Ebenen (Parameterform und Koordinatenform) wird die Schnittgerade berechnet und veranschaulicht.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (15): [5:30]
Anschaulich vorgeführt wird die Berechnung des Abstands eines Punktes im Raum (R^3) zu einer Ebene durch das Lotfußpunktverfahren.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (16): [3:49]
Anschaulich beschrieben und vorgerechnet wird ein Beispiel zur Abstandsberechnung eines Punktes zu einer Geraden im Raum (R^3) nach dem Lotfußpunktverfahren.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analytische Geometrie (17): [4:57]
Anschaulich beschrieben und vorgerechnet wird ein Beispiel zur Abstandsberechnung zweier windschiefer Geraden im Raum (R^3) nach dem Lotfußpunktverfahren.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
siehe auch: Themenseite - Analytische Geometrie
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)