Regelheft (1)
Regelheft (DIN-A6, 2. Auflage) (ISBN 978-3-750248-16-8 → Publikationen)



Teilermengen und Primzahlen: [5:09]
Anschauliche Bestimmung der Elemente einer Teilermenge. Weiterhin wird die Bedeutung des Begriffs "Primzahlen" verdeutlicht.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.



Grundrechenarten - Addition (a): [4:55]
Gezeigt wird die Addition von natürlichen Zahlen an Beispielen.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Grundrechenarten - Addition (b): [3:09]
Gezeigt wird die Addition von Dezimalzahlen (Dezimalbrüchen) an Beispielen.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Grundrechenarten - Subtraktion: [7:51]
Grundrechenarten: Gezeigt wird die Subtraktion von Zahlen an Beispielen.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Grundrechenarten - Multiplikation (a): [3:34]
Gezeigt wird die Multiplikation von Zahlen am Beispiel 324*8. (Mehrstellige Zahl mal einstelligen Zahl).
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Grundrechenarten - Multiplikation (b): [7:14]
Gezeigt wird die Multiplikation von Zahlen am Beispiel 3729*625. (Mehrstellige Zahl mal mehrstellige Zahl).
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Grundrechenarten - Division (a): [6:19]
Gezeigt wird die Division von Zahlen am Beispiel 4675:8. Dabei wird die Rechnung mit einem Rest beendet. (natürliche Zahlen)
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Grundrechenarten - Division (b): [4:28]
Gezeigt wird die Division von Zahlen am Beispiel 4675:8. Dabei wird die Rechnung aus dem ersten Video fortgesetzt und das exakte Ergebnis berechnet - mit Nachkommastellen. (rationale Zahlen)
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................


Grundlagen - Rechengesetze: [4:44]
Multiplikation - Rechengesetze & Anwendungen
Grundrechenarten - Rechenvorteile bei der Multiplikation mit Stufenzahlen. Es werden Anwendungsbeispiele für Rechnungen mit Stufenzahlen gezeigt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Grundlagen - Rechengesetze: [5:05]
Verteilungsgesetz (Distributivgesetz)
Gezeigt wird die Anwendung des Distributivgesetzes (Verteilungsgesetzes) an einem einfachen Beispiel. Erklärt wird das Ausklammern und Ausmultiplizieren zur Umformung von Rechenausdrücken.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

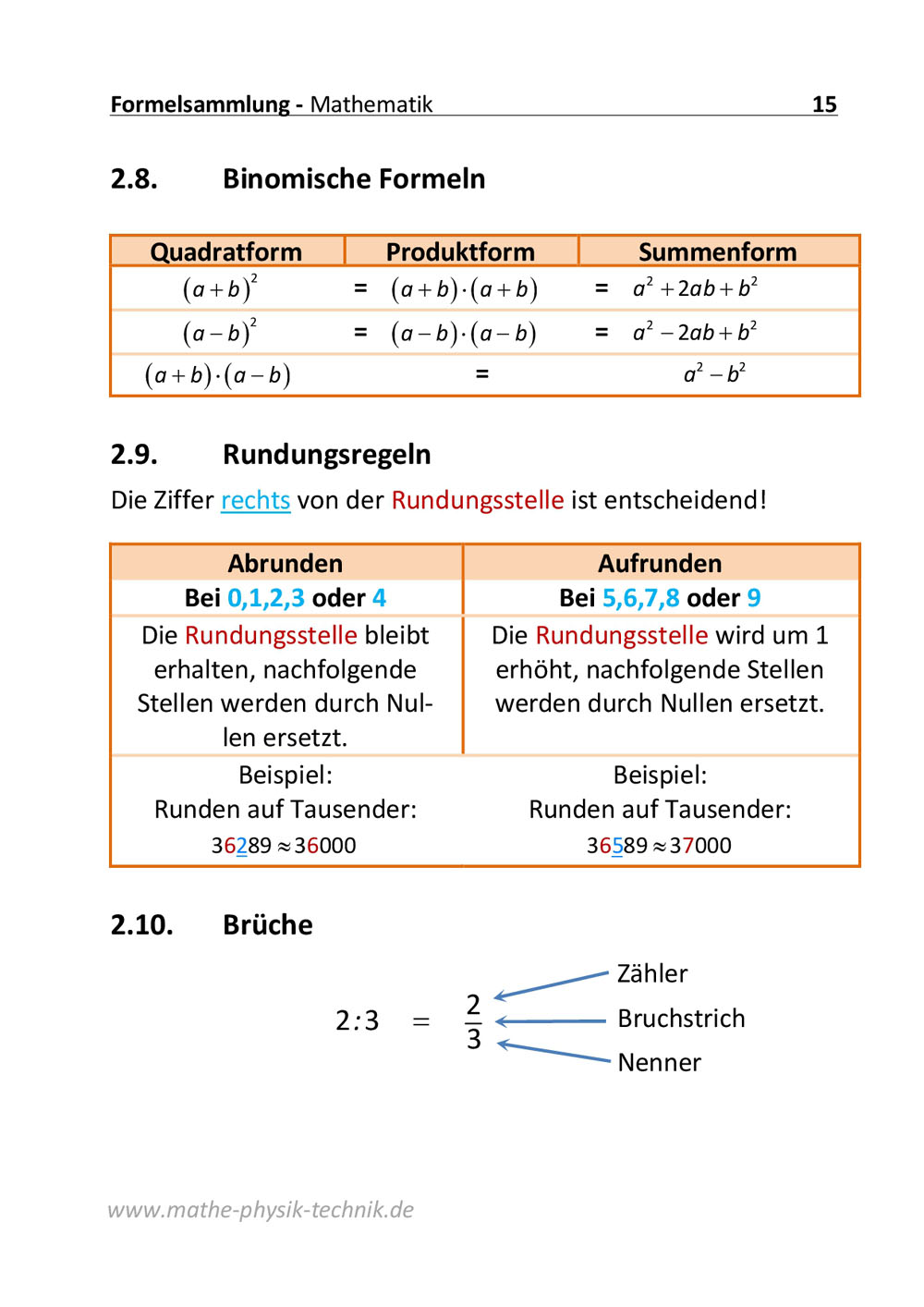

Gleichungen: Binomische Formeln (1) [2:49]
Teil 1 - Erste binomische Formel
Anschaulich hergeleitet werden die binomischen Gleichungen durch geometrische Überlegungen. [ Binome, Binom ]
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Gleichungen: Binomische Formeln (2) [3:48]
Teil 2 - Zweite binomische Formel
Anschaulich hergeleitet werden die binomischen Gleichungen durch geometrische Überlegungen. [ Binome, Binom ]
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Gleichungen: Binomische Formeln (3) [3:22]
Teil 3 - Dritte binomische Formel
Anschaulich hergeleitet werden die binomischen Gleichungen durch geometrische Überlegungen. [ Binome, Binom ]
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................


Bruchrechnung: [11:53]
Teil 1: Brüche darstellen, erweitern und kürzen
Die Darstellung und Schreibweise von Brüchen wird erklärt. Beispiele zeigen anschauliche Anwendungen. Weiterhin werden Umformungen vorgeführt: Brüche werden erweitert und gekürzt - mit Beispielen.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Bruchrechnung: [9:00]
Teil 2: Brüche addieren und subtrahieren
Mathematik - Bruchrechnung (Teil 2) - Die Grundrechenarten der Addition und Subtraktion werden an Beispielen anschaulich erklärt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................
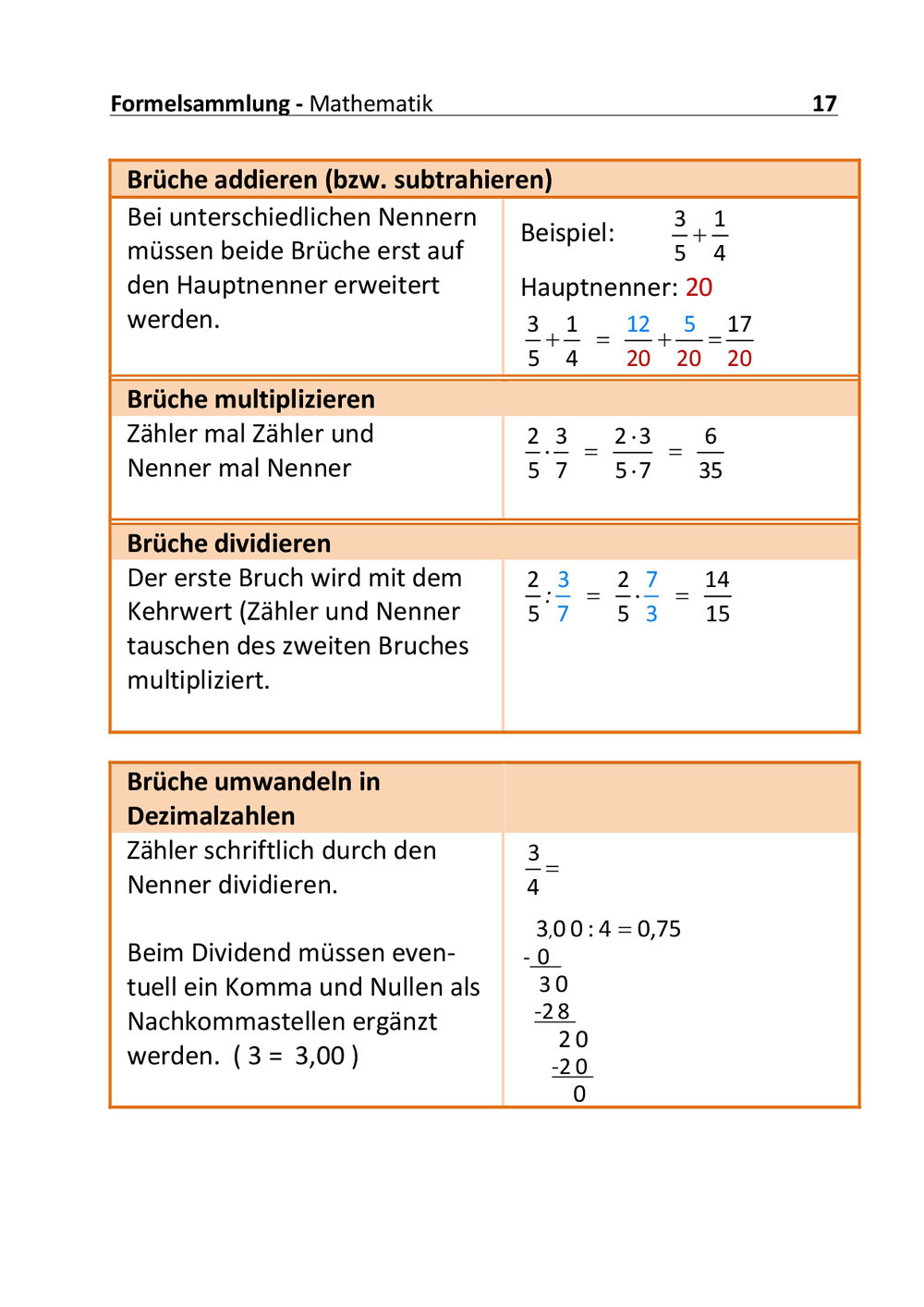

Bruchrechnung: [7:18]
Teil 3: Brüche multiplizieren
Bruchrechnung (Teil 3) - Die Multiplikation von Brüchen wird an Beispielen anschaulich erklärt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Bruchrechnung: [8:05]
Teil 4: Brüche dividieren
Mathematik - Bruchrechnung (Teil 4) - Die Division von Brüchen wird an Beispielen anschaulich erklärt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Bruchrechnung: [7:18]
Teil 3: Brüche multiplizieren
Bruchrechnung (Teil 3) - Die Multiplikation von Brüchen wird an Beispielen anschaulich erklärt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Bruchrechnung: [8:05]
Teil 4: Brüche dividieren
Mathematik - Bruchrechnung (Teil 4) - Die Division von Brüchen wird an Beispielen anschaulich erklärt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Bruchrechnung: [5:37]
Teil 6: Dezimalbrüche und Dezimalzahlen
Beschrieben und anschaulich vorgeführt werden die Eigenschaften von Dezimalbrüchen und die Umwandlung in Dezimalzahlen.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
................................................
siehe auch: Video → Zehnersystem / Stellenwerttafel
................................................


Zehnersystem - Stellenwerttafel: [5:50]
Das Zehnersystem und die Handhabung der Stellenwerttafel werden an Beispielen vorgeführt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.


Geometrie - Flächeneinheiten: [6:14]
Flächeneinheiten und Umrechnungen
Die Umrechnung von Flächeneinheiten wird vorgeführt. Veranschaulicht wird dabei die Umrechnungszahl 100. Flächeneinheiten für große und gleine Flächeninhalte werden eingeführt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Geometrie - Volumenberechnung (1): [5:45]
Volumenformel für den Quader /
Volumeneinheit: Kubikzentimeter
Die Berechnung des Volumens eines Quaders wird anschaulich dargestellt. Zwei verschiedene Quader werden mit Kubikzentimeterwürfeln aufgefüllt, dadurch das Volumen bestimmt und die Einheit "Kubikzentimeter" dadurch eingeführt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Geometrie - Volumenberechnung (2): [6:20]
Volumeneinheiten und Umrechnungen
Die zur Angabe des Volumens eines Quaders notwendigen Einheiten (Kubikzentimeter, Kubikdezimeter, etc.) und deren Zusammenhänge werden anschaulich dargestellt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Experimentelle Verfahren zur Volumenbestimmung werden in den Videobeiträgen zum Differenzenverfahren und zum Überlaufverfahren gezeigt.
........................................................................................................
Hier geht's zum → Lern-Archiv

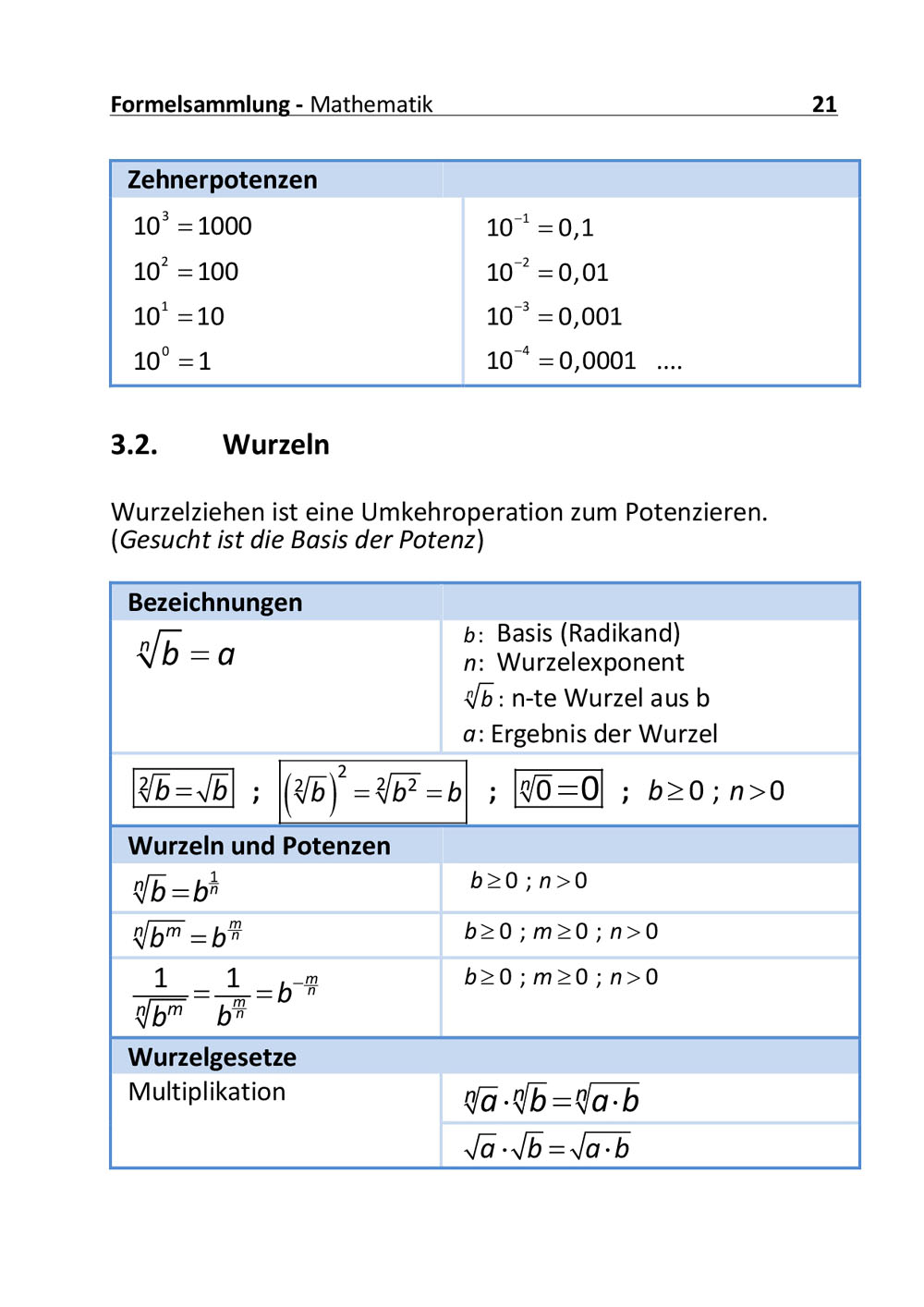



Zuordnungen (1): Darstellungsformen [4:57]
Zuordnungen werden an einfachen Beispielen eingeführt und verschiedene Darstellungsarten für Zuordnungen gezeigt (Tabelle, Pfeildiagramm, grafische Darstellung im Koordinatensystem, Wortform).
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
(→ Übungsblatt)
........................................................................................................

Zuordnungen (2): Proportionale Zuordnungen [5:25]
Proportionale Zuordnungen werden beschrieben, berechnet und grafisch veranschaulicht (steigende Halbgeraden). Weiterhin wird die Quotientengleichheit gezeigt und der Proportionalitätsfaktor berechnet.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
(→ Übungsblatt)
........................................................................................................


Zuordnungen (3): Antiproportionale Zuordnungen [4:58]
Antiproportionale Zuordnungen werden beschrieben, berechnet und grafisch veranschaulicht (Hyperbel). Weiterhin wird die Produktgleichheit gezeigt und der Proportionalitätsfaktor berechnet.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
(→ Übungsblatt)
........................................................................................................
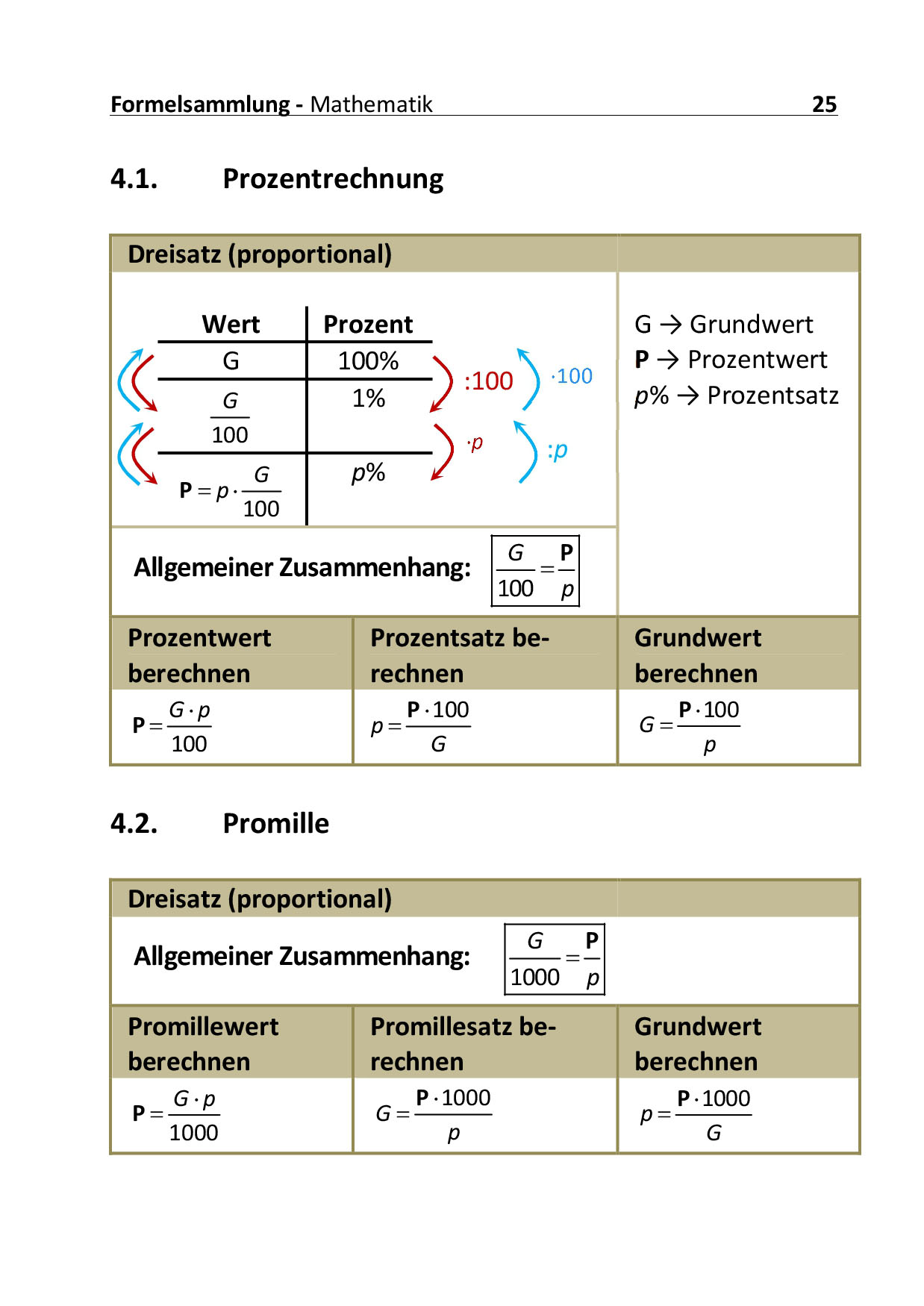
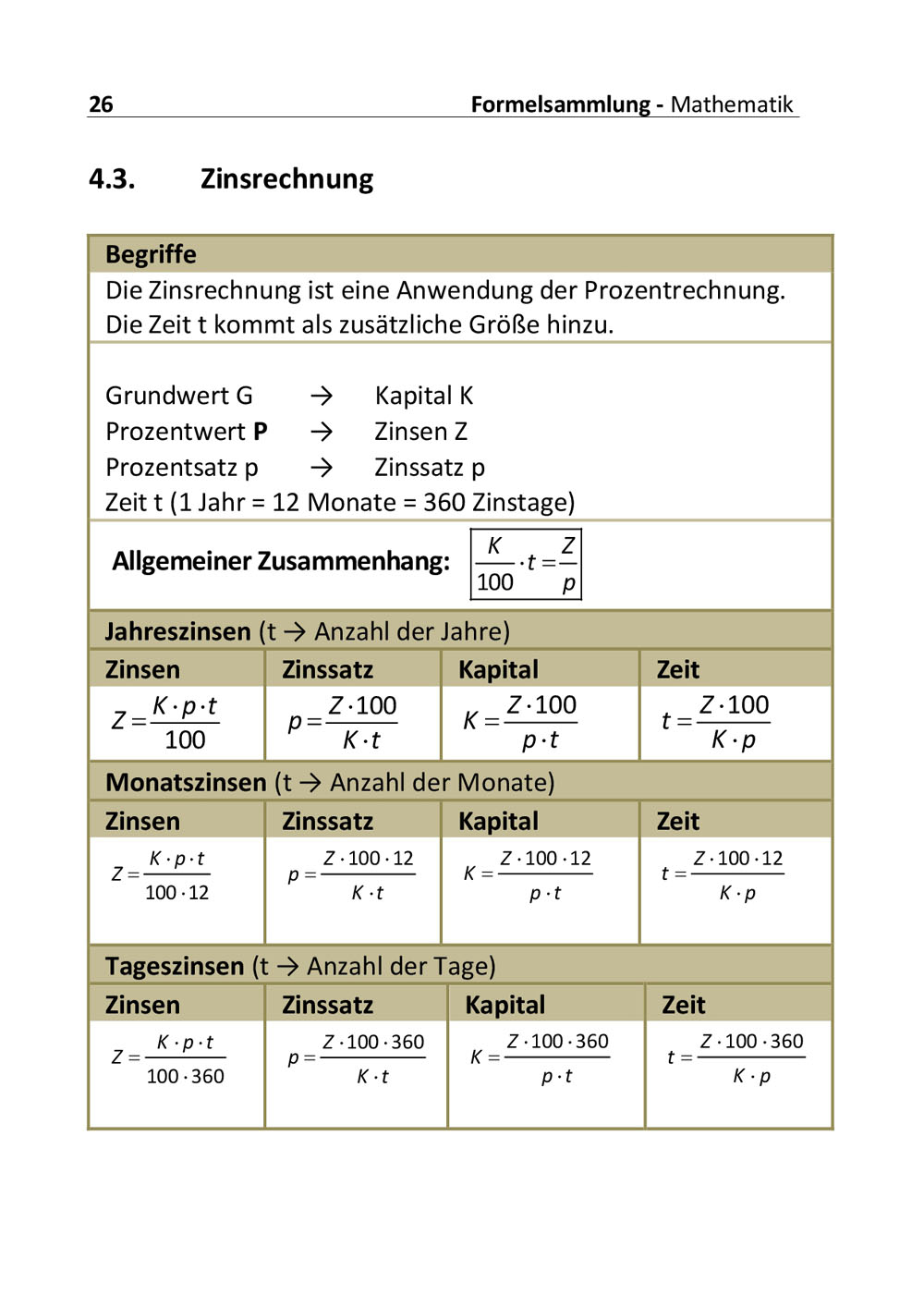


Funktionen: Wachstum und Abnahme (1): [6:34]
Lineare Wachstums- und Abnahmevorgänge
Im ersten Teil wird additives und subtraktives Wachstum an Beispielen erklärt. Die Wachstumsformel für lineares Wachstum und Abnahme wird hergeleitet. Die Beispiele werde dann auch grafisch dargestellt.

Funktionen: Wachstum und Abnahme (2): [8:48]
Wachstumsrate und Wachstumsfaktor
Die Begriffe Wachstumsrate (Abnahmerate) und Wachstumsfaktor (Abnahmefaktor) werden an Beispielen hergeleitet und erklärt. Abschließend wird ein Anwendungsbeispiel in schülerüblicher Schreibweise vorgeführt.

Funktionen: Wachstum und Abnahme (3): [11:34]
Exponentielle Wachstums- und Abnahmevorgänge
Im dritten Teil werden exponentielle Vorgänge, also multiplikative Zu- und Abnahme an Beispielen erklärt. Die Wachstumsformel für exponentielles Wachstum und Abnahme wird hergeleitet. Die Beispiele werde dann auch grafisch dargestellt.
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)



Funktionen: Lineare Funktionen (1) [6:07]
Veranschaulicht wird der Funktionsbegriff und wie über eine Wertetabelle allgemein eine Funktion in einem Diagramm mithilfe der Funktionsgleichung dargestellt werden kann.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
(→ Übungsblatt)
........................................................................................................

Funktionen: Lineare Funktionen (2) [5:52]
Veranschaulicht werden lineare Funktionen die durch den Ursprung verlaufen (y = m * x). An Beispielen werden Funktionsgleichungen systematisch verändert und so der Zugang zu linearen Funktionsgraphen erreicht.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
(→ Übungsblatt)
........................................................................................................

Funktionen: Lineare Funktionen (3) [5:56]
Veranschaulicht werden allgemeine lineare
Funktionen (y = m * x + n).
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
(→ Übungsblatt)
........................................................................................................

Funktionen: Lineare Funktionen (4) [5:41]
Lineare Funktionen im Koordinatensystem darstellen
An Beispielen wird demonstriert wie lineare Funktionen nach Vorgabe der Funktionsgleichung ins Koordinatensystem eingezeichnet werden.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
(→ Übungsblatt)
........................................................................................................

Funktionen: Lineare Funktionen (5) [7:51]
Das Steigungsdreieck (1)
An Beispielen wird die Handhabung des Steigungsdreiecks bei linearen Funktionen demonstriert. Die Steigung ist in den Beispielen jew. ganzzahlig. Nach Vorgabe der Funktionsgleichung werden die Funktionen ins Koordinatensystem eingezeichnet werden.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
(→ Übungsblatt)
........................................................................................................

Funktionen: Lineare Funktionen (6) [6:18]
Das Steigungsdreieck (2)
An Beispielen wird die Handhabung des Steigungsdreiecks bei linearen Funktionen demonstriert. Die Steigung ist in den Beispielen jew. eine Bruchzahl. Nach Vorgabe der Funktionsgleichung werden die Funktionen ins Koordinatensystem eingezeichnet werden.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
(→ Übungsblatt)
........................................................................................................
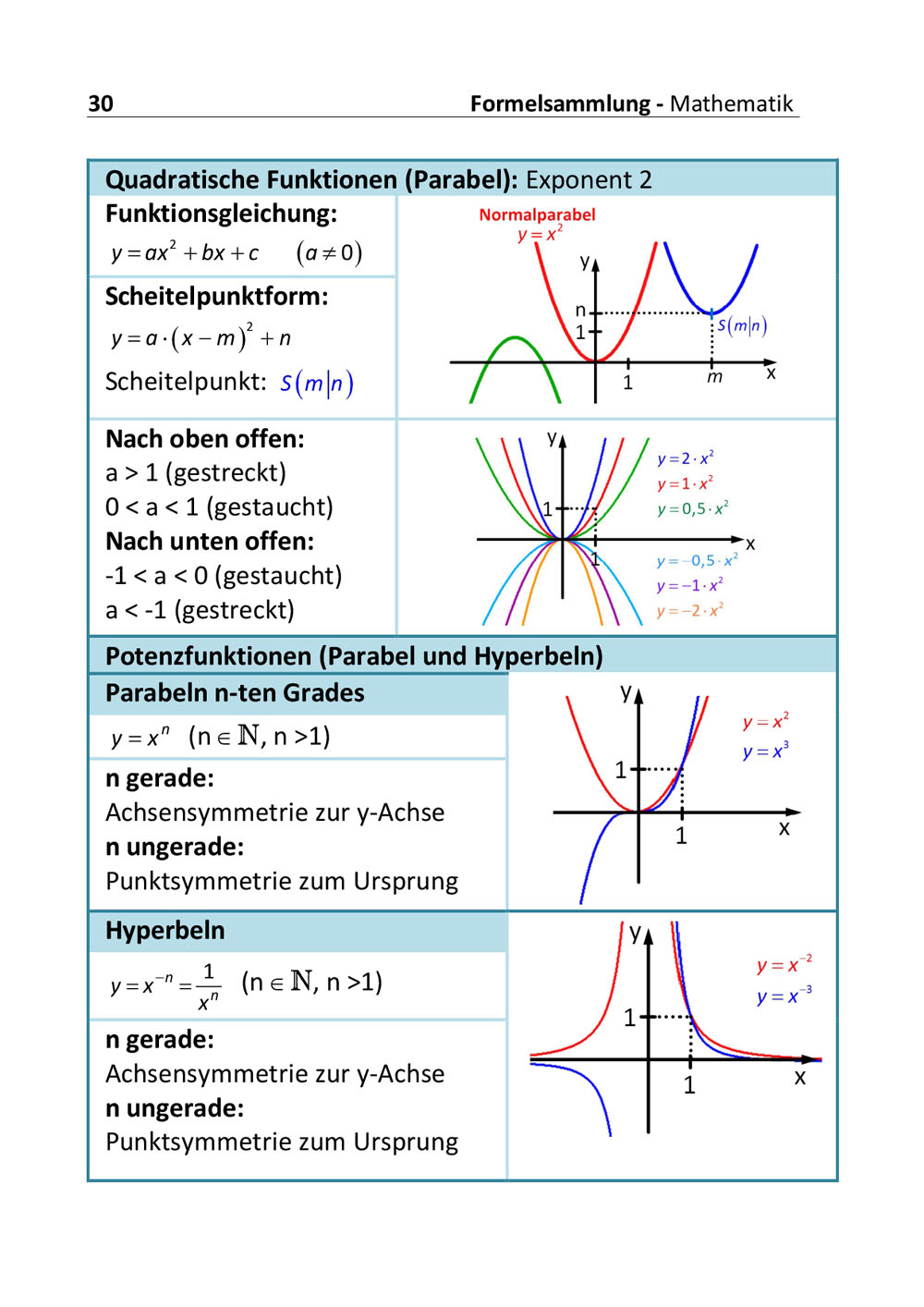

Funktionen: Quadratische Funktionen (1) [4:18]
Quadratische Funktionen vom Typ f(x)=x2+c.
Ausgehend von der Normalparabel werden Verschiebungen in y-Richtung veranschaulicht und begründet.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
(→ Übungsblatt)
Vorausgesetzte Grundlagen für die Videos
zu quadratischen Funktionen sind: Lineare Funktionen
........................................................................................................

Funktionen: Quadratische Funktionen (2) [3:35]
Quadratische Funktionen vom Typ f(x)=(x+b)2+c.
Ausgehend von der Normalparabel werden Verschiebungen in x-Richtung veranschaulicht und begründet. Anschließend werden zusammengesetzte Verschiebungen an Beispielen gezeigt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
(→ Übungsblatt)
........................................................................................................

Funktionen: Quadratische Funktionen (3) [6:19]
Quadratische Funktionen vom Typ f(x)=a(x+b)2+c.
Ausgehend von der Normalparabel werden Verschiebungen gestauchte und gestreckte Parabeln veranschaulicht und begründet.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
(→ Übungsblatt)
........................................................................................................
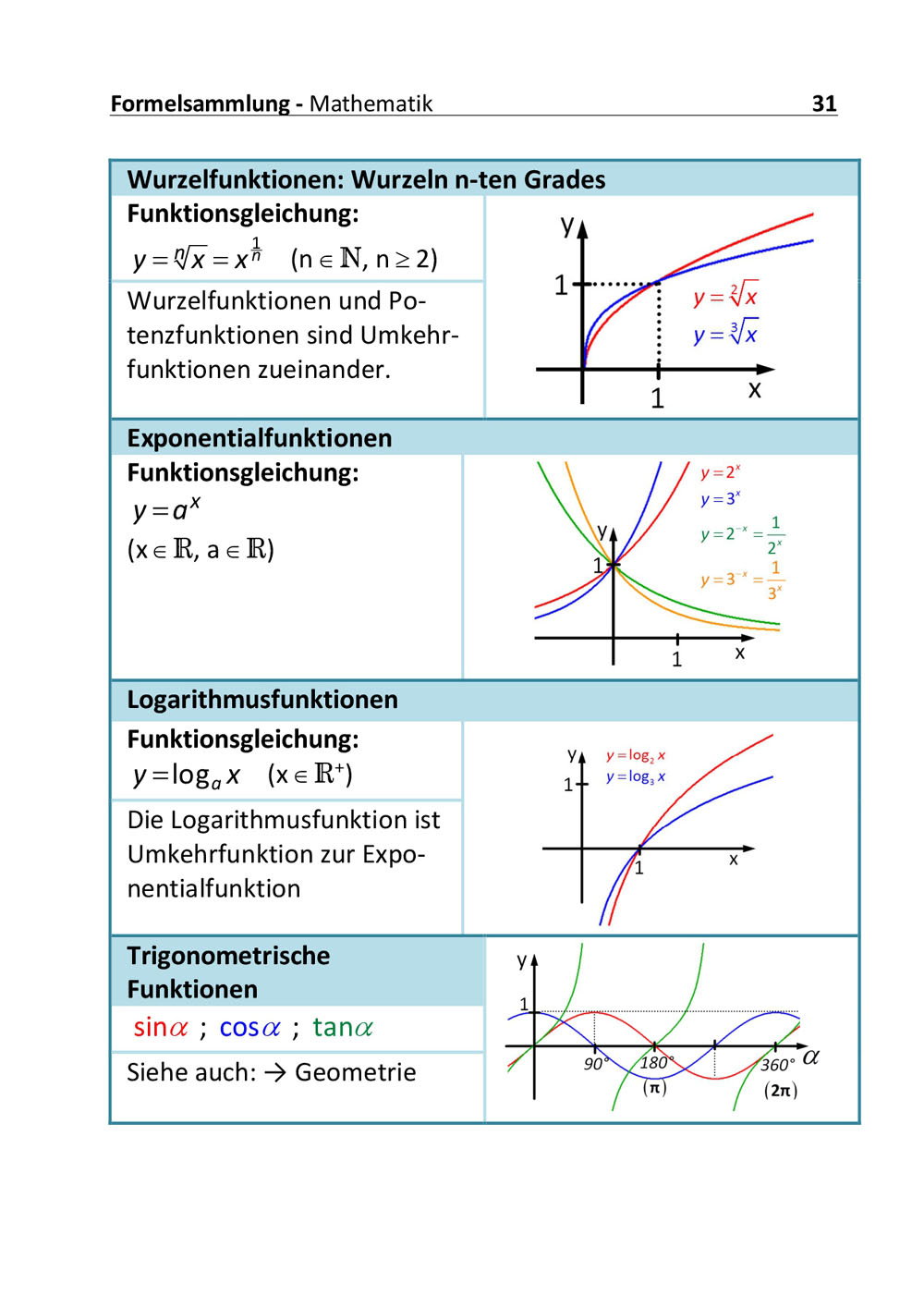

Funktionen: Trigonometrische Funktionen: [7:10]
Die Sinusfunktion am Einheitskreis
Ausgehend von der Definition der trigonometrischen Funktionen wird die Sinusfunktion anschaulich am Einheitskreis entwickelt.
........................................................................................................

Funktionen: Exponentielles Wachstum und Abnahme: [4:46]
Zwei Anwendungsbeispiele
Mathematik - Exponentielles Wachstum und Abnahme - Es werden zwei Anwendungsbeispiele (bakterielles Wachstum, radioaktiver Zerfall) vorgerechnet und wichtige Begriffe erklärt:
Wachstumsformel, Wachstumsfaktor, Wachstumsrate, Abnahmeformel, Abnahmefaktor, Abnahmerate
.......................................................................................................

Funktionen: Exponentialfunktionen [5:40]
Eigenschaften von Exponentialfunktionen
Die grundlegenden Eigenschaften von Exponentialfunktionen werden beschrieben.
........................................................................................................

Funktionen: Logarithmusfunktionen [1] [6:37]
Eigenschaften von Logarithmusfunktionen
Wie ändert sich der Funktionsgraph durch systematische Änderungen der Funktionsgleichungen?
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Funktionen: Logarithmusfunktionen [2] [2:14]
Zusammenhang zwischen Exponential- und Logarithmusfunktionen
Dargestellt wird der Zusammenhang zwischen Logarithmus- und Exponentialfunktionen durch Bildung der Umfehrfunktion.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
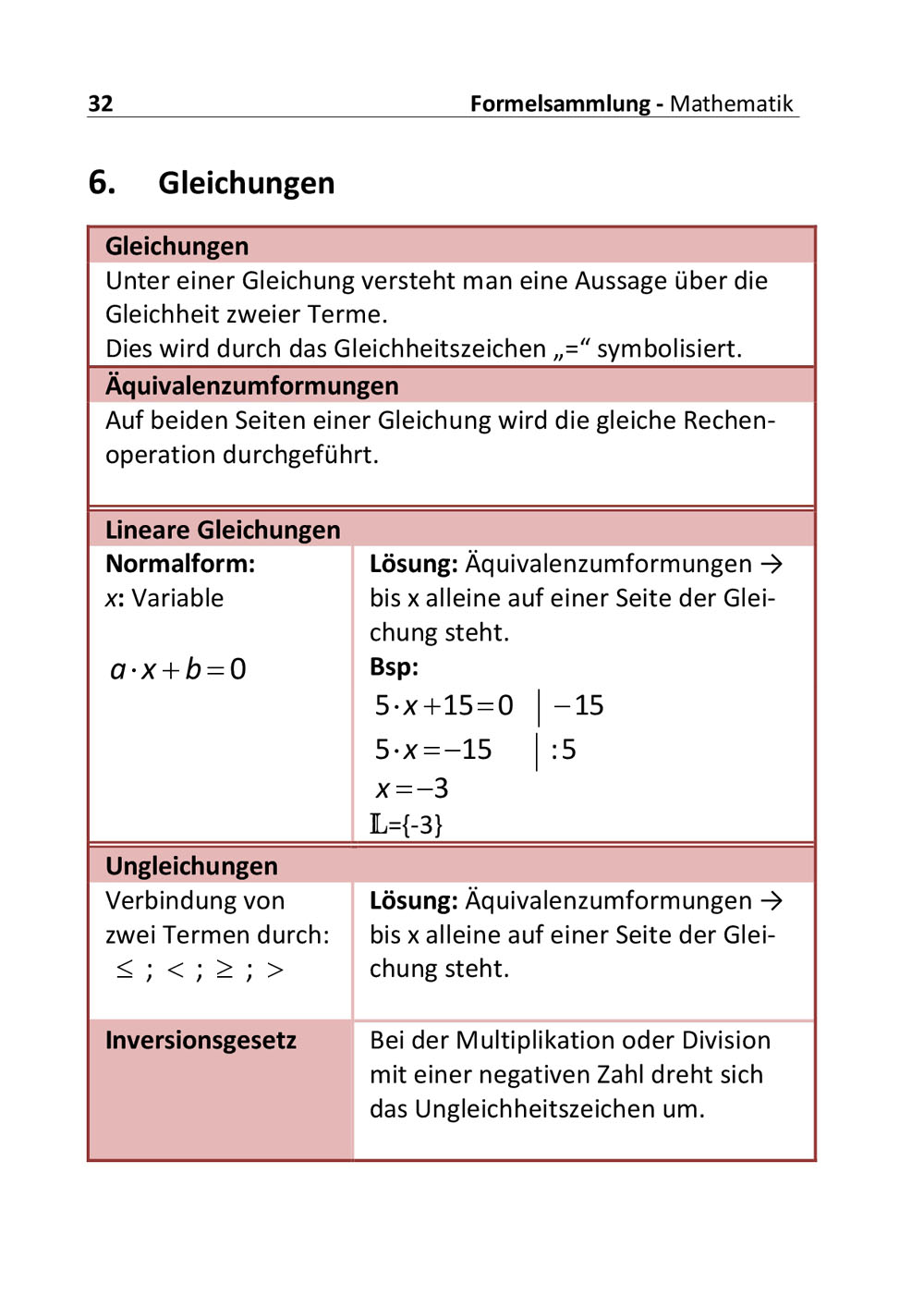


Gleichungen: Quadratische Gleichungen (1) [5:10]
Lösung quadratischer Gleichungen vom Typ x2+c=0
An Beispielen wird das zeichnerische und rechnerische Lösungsverfahren für quadratische Gleichungen des Typs x2+c=0 gezeigt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Vorausgesetzte Grundlagen für die Videos zu quadratischen Gleichungen sind: Lineare Funktionen und quadratische Funktionen, Weiterhin werden Kenntnisse zu binomischen Formeln für die Rechnungen benötigt.
........................................................................................................

Gleichungen: Quadratische Gleichungen (2) [5:50]
Lösung quadratischer Gleichungen vom Typ x2+bx=0
An Beispielen wird das zeichnerische und rechnerische Lösungsverfahren für quadratische Gleichungen des Typs x2+bx=0 gezeigt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Gleichungen: Quadratische Gleichungen (3) [7:34]
Lösung quadratischer Gleichungen vom Typ ax2+bx+c=0
An Beispielen wird das zeichnerische Lösungsverfahren für quadratische Gleichungen des Typs ax2+bx+c=0 gezeigt. Weiterhin werden die a-b-c-Formel und die p-q-Formel als rechnerische Lösungsmethode vorgestellt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Gleichungen: Quadratische Gleichungen (4) [5:38]
Herleitung der p-q-Formel für Gleichungen des Typs x2+px+q=0
Die p-q-Formel wird durch die quadratische Ergänzung schrittweise hergeleitet und anschließend ein Beispiel gerechnet.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................


Lineare Gleichungssysteme (3) [5:08]
Rechnerische Lösung: Das Additionsverfahren
Das Additionsverfahren für lineare Gleichungssysteme wird erklärt und an einem Beispiel vorgeführt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................






























