Mathematik - Grundlagen [2/7]

Videos (YouTube):

Gleichungen: Binomische Formeln (1) [2:49]

Teil 1 - Erste binomische Formel

Anschaulich hergeleitet werden die binomischen Gleichungen durch geometrische Überlegungen.

→ Übungsblätter 

Gleichungen: Binomische Formeln (2) [3:48]
Teil 2 - Zweite binomische Formel

Anschaulich hergeleitet werden die binomischen Gleichungen durch geometrische Überlegungen.

→ Übungsblätter 

Gleichungen: Binomische Formeln (3) [3:22]
Teil 3 - Dritte binomische Formel

Anschaulich hergeleitet werden die binomischen Gleichungen durch geometrische Überlegungen. 

→ Übungsblätter 

Diese App ist ein Derivat einer App von regina hess bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App ist ein Derivat einer App von Barbara Sönser bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App ist ein Derivat einer App von Barbara Sönser bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App ist ein Derivat einer App von brunnen bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App ist ein Derivat einer App von brunnen bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App ist ein Derivat einer App von brunnen bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App wurde erstellt von Dr. Andreas Rueff (Lernplattform www.mathe-physik-technik.de) bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App ist ein Derivat einer App von herr_mauthe bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App ist ein Derivat einer App von taraxacum bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App ist ein Derivat einer App von Thomas Kroll bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App ist ein Derivat einer App von b3n1337 bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Videos (YouTube):

Gleichungen: Quadratische Gleichungen (1) [5:10]
Lösung quadratischer Gleichungen vom Typ x²+c=0

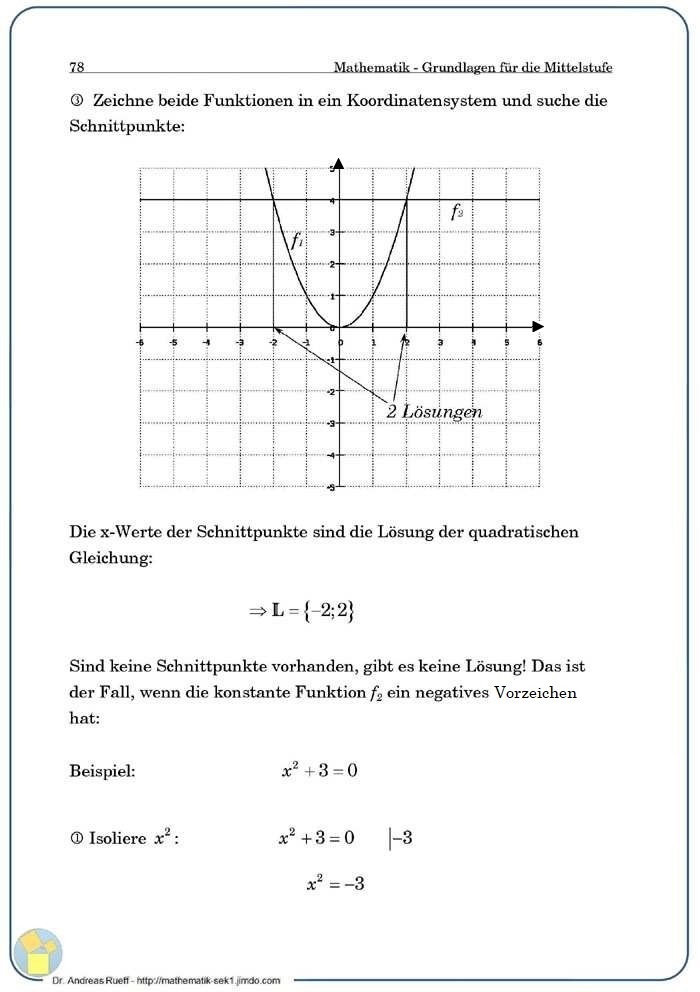
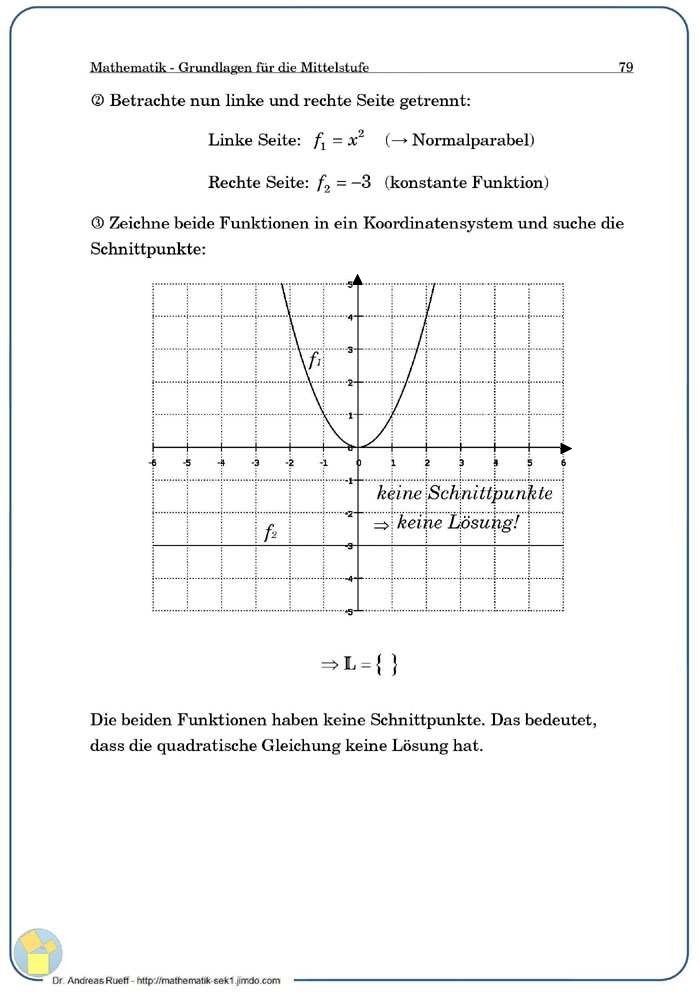
An Beispielen wird das zeichnerische und rechnerische Lösungsverfahren für quadratische Gleichungen des Typs x²+c=0 gezeigt.

→ Übungsblätter 

 

Vorausgesetzte Grundlagen für die Videos zu quadratischen Gleichungen sind: Lineare Funktionen und quadratische Funktionen, Weiterhin werden Kenntnisse zu binomischen Formeln für die Rechnungen benötigt.

Diese App ist ein Derivat einer App von lisawegele bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Videos (YouTube):

Gleichungen: Quadratische Gleichungen (2) [5:50]
Lösung quadratischer Gleichungen vom Typ x²+bx=0

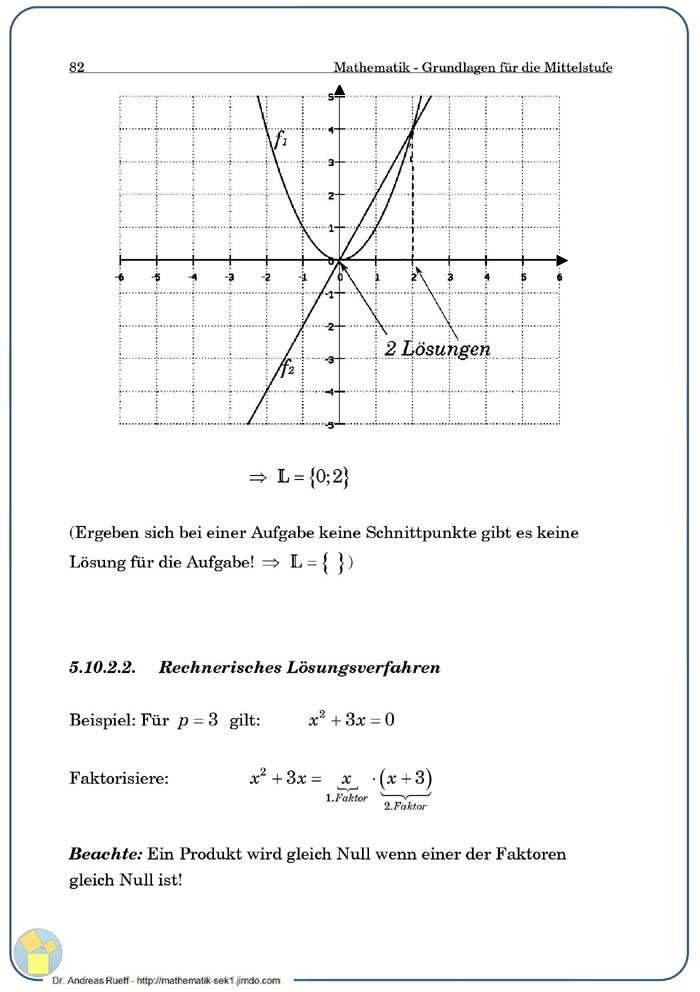
An Beispielen wird das zeichnerische und rechnerische Lösungsverfahren für quadratische Gleichungen des Typs x²+bx=0 gezeigt.

Anmerkung: Im Buch wird diese Form als "x²+px=0" beschreiben, im Video wird als Variable anstelle des "p" ein "b" verwendet: x²+bx=0 .

→ Übungsblätter 

Videos (YouTube):

Gleichungen: Quadratische Gleichungen (3) [7:34]
Lösung quadratischer Gleichungen vom Typ ax²+bx+c=0

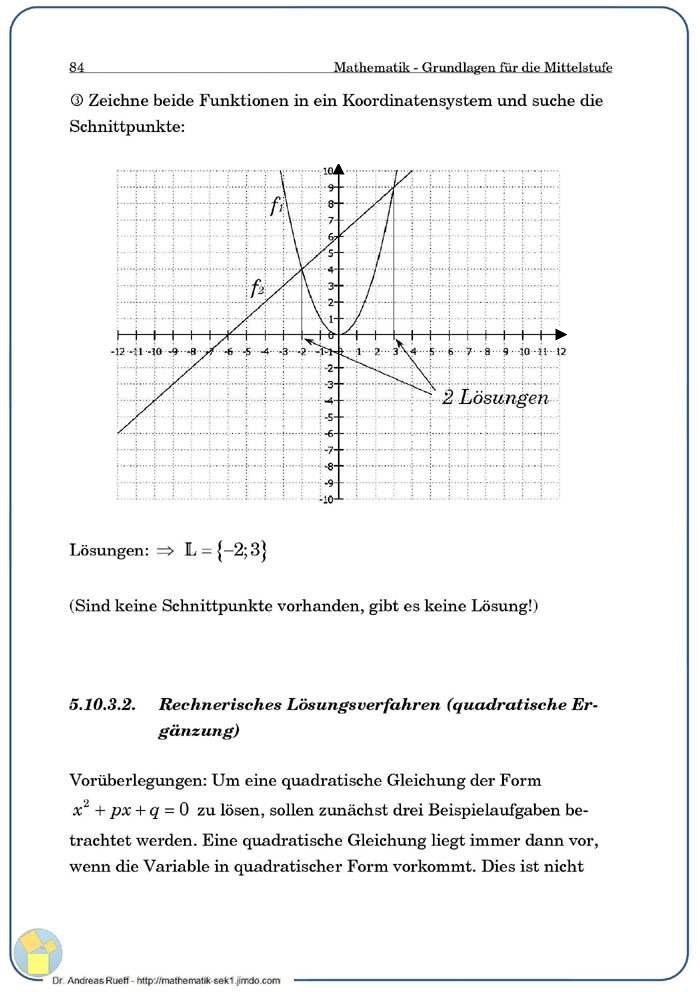
An Beispielen wird das zeichnerische Lösungsverfahren für quadratische Gleichungen des Typs ax²+bx+c=0 gezeigt. Weiterhin werden die a-b-c-Formel und die p-q-Formel als rechnerische Lösungsmethode vorgestellt.

→ Quadratische Gleichungen

→ Übungsblätter 

........................................................................................................

Diese App ist ein Derivat einer App von lisawegele bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App ist ein Derivat einer App von Christian Klingert bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App ist ein Derivat einer App von lisawegele bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Videos (YouTube):

Gleichungen: Quadratische Gleichungen (4) [5:38]
Herleitung der p-q-Formel für Gleichungen des Typs x²+px+q=0

Die p-q-Formel wird durch die quadratische Ergänzung schrittweise hergeleitet und anschließend ein Beispiel gerechnet.

→ Quadratische Gleichungen

→ Übungsblätter 

Videos (YouTube):

Gleichungen: Quadratische Gleichungen (5) [4:03]
Der Satz von Vieta 

Der Satz von Vieta wird an einem Beispiel vorgeführt und die allgemeine Handhabung erklärt.

Diese App ist ein Derivat einer App von Dagmar Herrmann bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App ist ein Derivat einer App von Bruno Sender bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

• Simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0 (https://phet.colorado.edu).

Aus dieser Seite sind Online-Übungen eingebunden. Diese sind bei www.learningapps.org erstellt worden, es kann sich auch teilweise um Apps von externen Erstellern handeln.