Mathematik - Übungsblätter (2)
( Nr. 11 - 20)
Mathematik:
Übungsheft zu den Grundlagen für die Mittelstufe
→ Übungsblätter (ISBN 9783744869126)
→ Lösungsheft (ISBN 9783744869607)
Hinweis:
Für den Unterricht ist die Anschaffung der Skripte und Bücher für meine Schüler nicht notwendig und nicht empfohlen! Die Übungsblätter werden bei Bedarf bearbeitet und notwendige Materialien
ggf. kopiert.

Teilermengen und Primzahlen: [5:09]
Anschauliche Bestimmung der Elemente einer Teilermenge. Weiterhin wird die Bedeutung des Begriffs "Primzahlen" verdeutlicht.


Bruchrechnung: [11:53]
Teil 1: Brüche darstellen, erweitern und kürzen
Die Darstellung und Schreibweise von Brüchen wird erklärt. Beispiele zeigen anschauliche Anwendungen. Weiterhin werden Umformungen vorgeführt: Brüche werden erweitert und gekürzt - mit Beispielen.


Bruchrechnung: [9:00]
Teil 2: Brüche addieren und subtrahieren
Mathematik - Bruchrechnung (Teil 2) - Die Grundrechenarten der Addition und Subtraktion werden an Beispielen anschaulich erklärt.
........................................................................................................

Bruchrechnung: [7:18]
Teil 3: Brüche multiplizieren
Bruchrechnung (Teil 3) - Die Multiplikation von Brüchen wird an Beispielen anschaulich erklärt.
........................................................................................................

Bruchrechnung: [8:05]
Teil 4: Brüche dividieren
Mathematik - Bruchrechnung (Teil 4) - Die Division von Brüchen wird an Beispielen anschaulich erklärt.
........................................................................................................

Bruchrechnung: [5:16]
Teil 5: Gemischte Zahlen
Beschrieben und anschaulich dargestellt wird im fünften Teil die Verwendung der Schreibweise gemischter Zahlen am Beispiel einer zerteilten Pizza.


Geometrie - Körpernetze (Abwicklungen): [3:16]
Beispiele: Quader und Würfel
Die Abwicklung eines Körpers zum Erhalt des Körpernetzes wird am Beispiel eines Quaders vorgeführt. Allgemeine Grundlagen zu Netzen werden zusammengefasst.
........................................................................................................

Geometrie - Schrägbilder: [6:47]
Gezeigt wird die Konstruktion von Schrägbildern - Mathematik, Mittelstufe. Dabei werden die grundlegenden Regeln eingeführt und beschreiben. Anschließend werden zwei Beispiele mit
allen notwendigen Einzelheiten vorgeführt: 1) Ein Quader und 2) ein Dreiecksprisma.
Diese Darstellungsart wird auch als Kabinett-Ansicht bezeichnet.
........................................................................................................

Bruchrechnung: [5:16]
Teil 5: Gemischte Zahlen
Beschrieben und anschaulich dargestellt wird im fünften Teil die Verwendung der Schreibweise gemischter Zahlen am Beispiel einer zerteilten Pizza.
........................................................................................................

Bruchrechnung: [5:37]
Teil 6: Dezimalbrüche und Dezimalzahlen
Beschrieben und anschaulich vorgeführt werden die Eigenschaften von Dezimalbrüchen und die Umwandlung in Dezimalzahlen.
................................................
siehe auch: Video → Zehnersystem / Stellenwerttafel
................................................


Grundlagen - Rechengesetze: [4:44]
Multiplikation - Rechengesetze & Anwendungen
Grundrechenarten - Rechenvorteile bei der Multiplikation mit Stufenzahlen. Es werden Anwendungsbeispiele für Rechnungen mit Stufenzahlen gezeigt.
........................................................................................................

Grundlagen - Rechengesetze: [5:05]
Verteilungsgesetz (Distributivgesetz)
Gezeigt wird die Anwendung des Distributivgesetzes (Verteilungsgesetzes) an einem einfachen Beispiel. Erklärt wird das Ausklammern und Ausmultiplizieren zur Umformung von Rechenausdrücken.


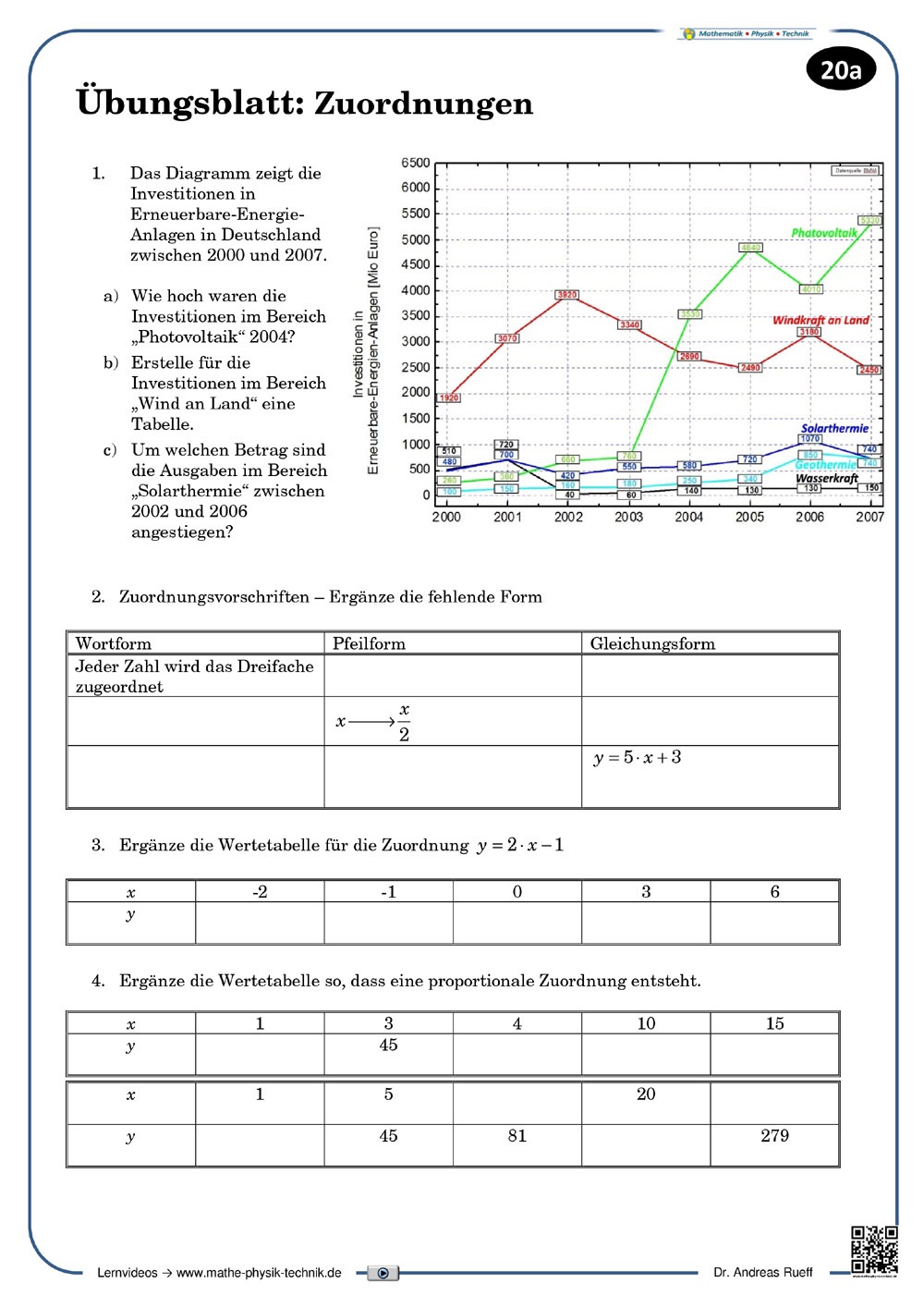
Zuordnungen (1): Darstellungsformen [4:57]
Zuordnungen werden an einfachen Beispielen eingeführt und verschiedene Darstellungsarten für Zuordnungen gezeigt (Tabelle, Pfeildiagramm, grafische Darstellung im Koordinatensystem, Wortform).
........................................................................................................

Zuordnungen (2): Proportionale Zuordnungen [5:25]
Proportionale Zuordnungen werden beschrieben, berechnet und grafisch veranschaulicht (steigende Halbgeraden). Weiterhin wird die Quotientengleichheit gezeigt und der Proportionalitätsfaktor berechnet.
........................................................................................................
 Die Arbeitsblätter auf dieser Seite sind lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Die Arbeitsblätter auf dieser Seite sind lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Übersicht der Rechen-Tools im → Lern-Archiv
und auf den → Themenseiten
1. Mathematik
Mini-Taschenrechner
Teilermenge / Primfaktorzerlegung
Potenzen
Berechnungen mit zwei Bruechen
Umwandlung: Bruch nach % oder Dezimal
Umwandlung: Prozent in Dezimalbruch und Bruch
Umwandlung: Dezimalbruch in Prozent und Bruch
Dezimalzahlen runden
Grundwert aus Prozentwert und Prozentsatz
Prozentsatz aus Grundwert und Prozentwert
Prozentwert aus Grundwert und Prozentsatz
Jahreszinsen
Monatszinsen
Tageszinsen
Zinseszinsen
Potenzen
Wurzeln berechnen
Logarithmus
Gleichungen
Gleichungen loesen (allg.)
Quadratische Gleichungen loesen
Gleichungssystem mit zwei Unbekannten
Gleichnungsystem mit drei Unbekannten
Funktionen
Wertetabelle erstellen
Funktionen darstellen (allg.)
Lineare Funktionen darstellen
Quadratische Funktionen darstellen
Proportionale Zuordnungen (Dreisatz)
Antiproportionale Zuordnungen
Exponentielles Wachstum/Abnahme (1)
Exponentielles Wachstum/Abnahme (2)
Exponentielles Wachstum/Abnahme (3)
Exponentielles Wachstum/Abnahme (4)
Exponentielles Wachstum/Abnahme (5)
Exponentielles Wachstum/Abnahme (6)
Trigonometrische Funktionen darstellen
Geometrie
Berechnungen am Zylinder
Berechnungen am Kegel
Berechnungen an der Kugel
Berechnungen am allgemeinen Dreieck (SSS)
Berechnungen am allgemeinen Dreieck (SWS)
Berechnungen am allgemeinen Dreieck (SWW)
Berechnungen am allgemeinen Dreieck (WSW)
Berechnungen - Pythagoras
Berechnungen am Kreis
Berechnungen an der Pyramide
Trigonometrie
Grad / Bogenmass
Trigonometrische Funktionen
Trigonometrische Umkehrfunktionen
Analysis
Folgen & Reihen
Polynomdivision berechnen
Taylorreihe
Riemannsche Summen
Grenzwerte berechnen
Berechnung der Ableitungsfunktion
Extremstellen berechnen
Berechnung des bestimmten Integrals
Berechnung des unbestimmten Integrals
Analytische Geometrie
Betrag eines Vektors
Abstandsformel im Raum R^3
Winkel zwischen zwei Vektoren
Addition von Vektoren
Subtraktion von Vektoren
Skalar-Multiplikation von Vektoren
Skalarprodukt von Vektoren
Kreuzprodukt von Vektoren
Umwandlung: Normalenform in Koordinatenform
Normalenvektor berechnen
Berechnung: Abstand Punkt - Ebene
Stochastik
Bernoulli / Binomialverteilung
Formel von Bernoulli B(n;p;k)
Kombinatorik - nPr
Kombinatorik - Binomialkoeffizienten (nCr)
Formel von Bernoulli / Binomialverteilung B(n;p;k)
Kumulierte Binomialverteilung F(n;p;k)
Normalverteilung zeichnen
3D-Funktionen darstellen
Komplexe Zahlen
Rechnen mit komplexen Zahlen (C)
Umwandeln: Polarform einer komplexen Zahl
2. Physik/Technik
Vorsaetze fuer Masseinheiten
Umrechnen: Laengeneinheiten
Umrechnen: Flaecheneinheiten
Umrechnen: Volumeneinheiten
Umrechnen: Zeiteinheiten
Umrechnung: Masseeinheiten
Umrechnen: Druckeinheiten
Umrechnungen: Dichteeinheiten
Umrechnung: Temperatureinheiten
Umrechnung: Leistungseinheiten
Umrechnung: Energieeinheiten
Zahlensysteme umrechnen
Boolesche Algebra (1) - Wahrheitstabellen
Boolesche Algebra (2)
Logische Schaltungen
Sichtbarer Sternenhimmel nach Ort und Zeit
Himmelsausschnitt und Sternzeit
Naechste Finsternisse
Mondphase
Planeten- und Mondpositionen
Aktuelle Daten zu Himmelskoerpern
Brechung an transparenten Medien (Snellius)
Bildentstehung bei der Linse
Brechung am Prisma
Konkavspiegel (Hohlspiegel)
Konvexspiegel (Woelbspiegel)
Subtraktive Farbmischung
Energieverbrauch - Statistik
Energiegewinnung - Statistiken
Periodensystem der Elemente
Eigenschaften der Elemente
Spezifische Aktivitaet
Halbertszeit von Isotopen
Elementeigenschaften
Isotope
Zerfallsreihen
Standorte von Kernkraftwerken
Hohe Bauwerke
Brücken
Motorisierte Luftfahrt
Schnelle Flugzeuge
QR-Code Generator
Produktlinks (amazon.de):