Mathematik - Übungsblätter (3)
( Nr. 21 - 30)
Mathematik:
Übungsheft zu den Grundlagen für die Mittelstufe
→ Übungsblätter (ISBN 9783744869126)
→ Lösungsheft (ISBN 9783744869607)
Hinweis:
Für den Unterricht ist die Anschaffung der Skripte und Bücher für meine Schüler nicht notwendig und nicht empfohlen! Die Übungsblätter werden bei Bedarf bearbeitet und notwendige Materialien
ggf. kopiert.

Prozentrechnung (1) - Einstieg und Grundbegriffe [3:57]
Erklärt werden Grundlagen und Grundbegriffe der Prozentrechnung an zwei Beispielen.
........................................................................................................

Prozentrechnung (2) - Der Prozentwert [4:06]
Gezeigt werden zwei mögliche Berechnungswege für den Prozentwert: Die Verwendung der Formel oder das
Dreisatzverfahren.
........................................................................................................

Prozentrechnung (3) - Der Grundwert [4:31]
Gezeigt werden zwei mögliche Berechnungswege für den Grundwert: Die Verwendung der Formel oder das
Dreisatzverfahren.
........................................................................................................

Prozentrechnung (4) - Der Prozentsatz [4:17]
Prozentrechnung (4) - Der Prozentsatz
Gezeigt werden zwei mögliche Berechnungswege für den Prozentsatz: Die Verwendung der Formel oder das Dreisatzverfahren.
........................................................................................................

Prozentrechnung (5) - Vermehrter und verminderter Grundwert [4:33]
Gezeigt werden zwei Beispiele: Ein Beispiel für den vermehrten und ein Beispiel für den verminderten Grundwert und die
Berechnungen mit Hilfe des Dreisatzverfahrens.
........................................................................................................

Bruchrechnung: [11:53]
Teil 1: Brüche darstellen, erweitern und kürzen
Die Darstellung und Schreibweise von Brüchen wird erklärt. Beispiele zeigen anschauliche Anwendungen. Weiterhin werden Umformungen vorgeführt: Brüche werden erweitert und gekürzt - mit Beispielen.



Gleichungen: Binomische Formeln (1) [2:49]
Teil 1 - Erste binomische Formel
Anschaulich hergeleitet werden die binomischen Gleichungen durch geometrische Überlegungen.
........................................................................................................

Gleichungen: Binomische Formeln (2) [3:48]
Teil 2 - Zweite binomische Formel
Anschaulich hergeleitet werden die binomischen Gleichungen durch geometrische Überlegungen.
........................................................................................................

Gleichungen: Binomische Formeln (3) [3:22]
Teil 3 - Dritte binomische Formel
Anschaulich hergeleitet werden die binomischen Gleichungen durch geometrische Überlegungen.

Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise
(manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise
(manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!

Funktionen: Lineare Funktionen (1) [6:07]
Veranschaulicht wird der Funktionsbegriff und wie über eine Wertetabelle allgemein eine Funktion in einem Diagramm mithilfe der Funktionsgleichung dargestellt werden kann.
........................................................................................................

Funktionen: Lineare Funktionen (2) [5:52]
Veranschaulicht werden lineare Funktionen die durch den Ursprung verlaufen (y = m ∙ x). An Beispielen werden Funktionsgleichungen systematisch verändert und so der Zugang zu linearen Funktionsgraphen erreicht.
........................................................................................................

Funktionen: Lineare Funktionen (3) [5:56]
Veranschaulicht werden allgemeine lineare
Funktionen (y = m ∙ x + n).
........................................................................................................

Funktionen: Lineare Funktionen (4) [5:41]
Lineare Funktionen im Koordinatensystem darstellen
An Beispielen wird demonstriert wie lineare Funktionen nach Vorgabe der Funktionsgleichung ins Koordinatensystem eingezeichnet werden.
........................................................................................................

Funktionen: Lineare Funktionen (5) [7:51]
Das Steigungsdreieck (1)
An Beispielen wird die Handhabung des Steigungsdreiecks bei linearen Funktionen demonstriert. Die Steigung ist in den Beispielen jew. ganzzahlig. Nach Vorgabe der Funktionsgleichung werden die Funktionen ins Koordinatensystem eingezeichnet werden.
........................................................................................................

Funktionen: Lineare Funktionen (6) [6:18]
Das Steigungsdreieck (2)
An Beispielen wird die Handhabung des Steigungsdreiecks bei linearen Funktionen demonstriert. Die Steigung ist in den Beispielen jew. eine Bruchzahl. Nach Vorgabe der Funktionsgleichung werden die Funktionen ins Koordinatensystem eingezeichnet werden.
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise
(manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise
(manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
→ Grundlagen für die Mittelstufe, S. 99 ff.)

Lineare Gleichungssysteme (1) [4:25]
Rechnerische Lösung: Das Einsetzungsverfahren
Das Einsetzungsverfahren für lineare Gleichungssysteme wird erklärt und an einem Beispiel vorgeführt.
........................................................................................................

Lineare Gleichungssysteme (2) [4:23]
Rechnerische Lösung: Das Gleichsetzungsverfahren
Das Gleichsetzungsverfahren für lineare Gleichungssysteme wird erklärt und an einem Beispiel vorgeführt.
........................................................................................................

Lineare Gleichungssysteme (3) [5:08]
Rechnerische Lösung: Das Additionsverfahren
Das Additionsverfahren für lineare Gleichungssysteme wird erklärt und an einem Beispiel vorgeführt.
→ Additionsverfahren (→ Grundlagen für die Mittelstufe, Seite 102/103)
........................................................................................................

Lineare Gleichungssysteme (4) [3:33]
Das graphische Lösungsverfahren
Das graphische Lösungsverfahren für lineare Gleichungssysteme wird erklärt und an einem Beispiel vorgeführt.
........................................................................................................

Lineare Gleichungssysteme (5) [6:16]
Spezialfälle
Spezialfälle für lineare Gleichungssysteme werden erklärt und an Beispielen vorgeführt. Die Fälle "keine Lösung" und "unendlich viele Lösungen" werden an Beispielen demonstriert.


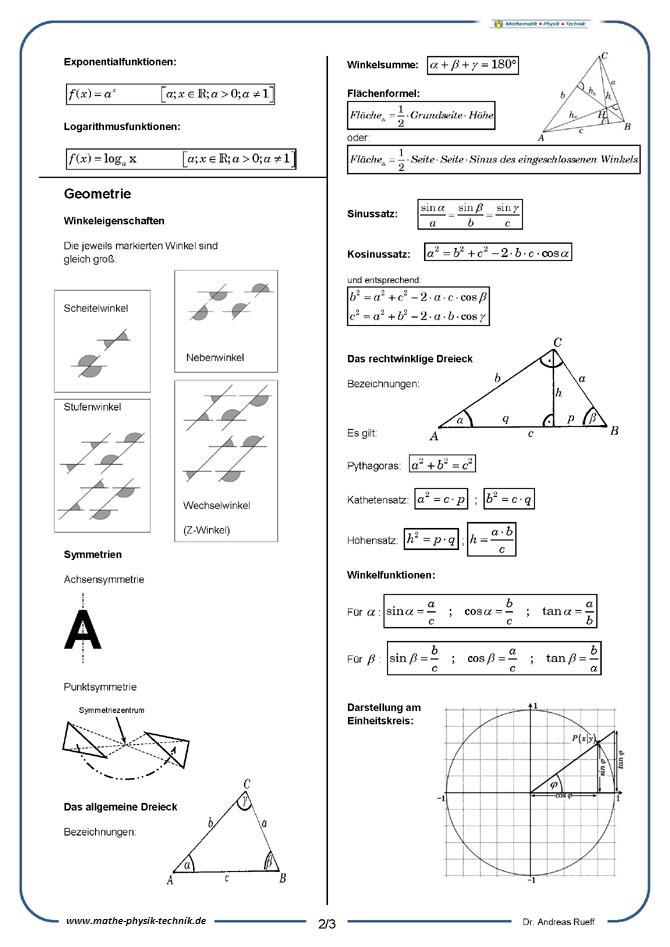
Geometrie: [2:45]
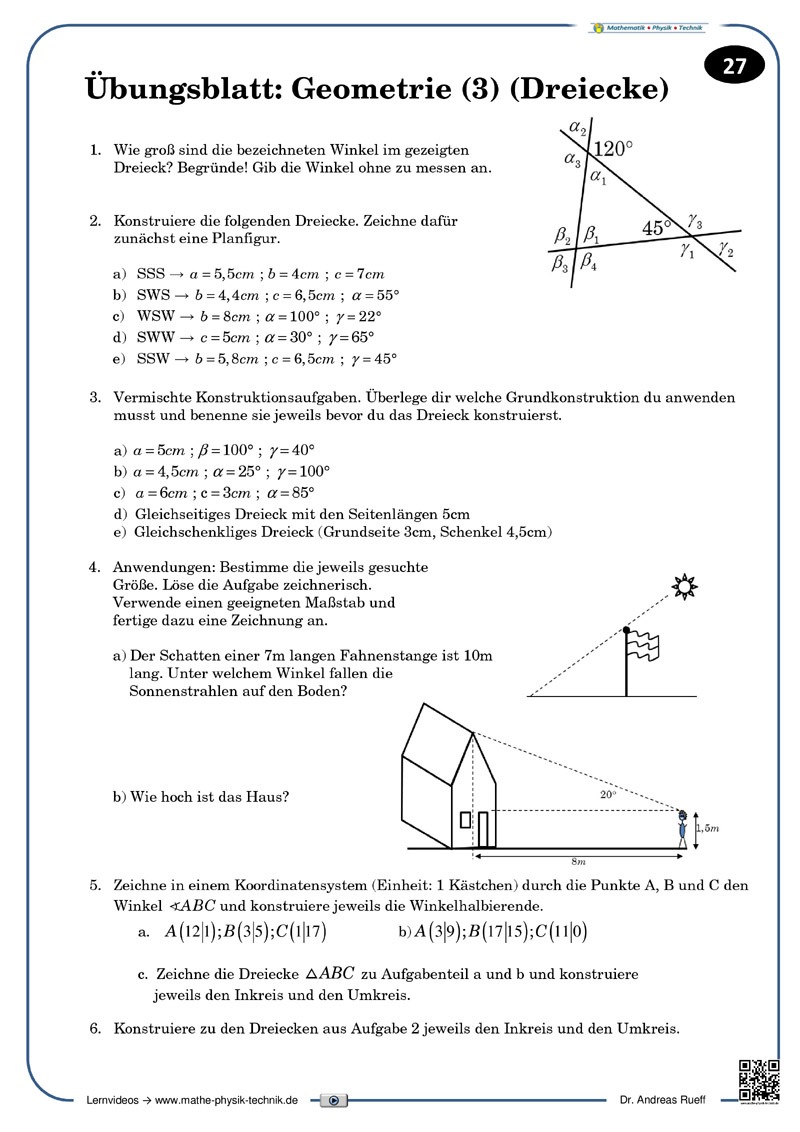
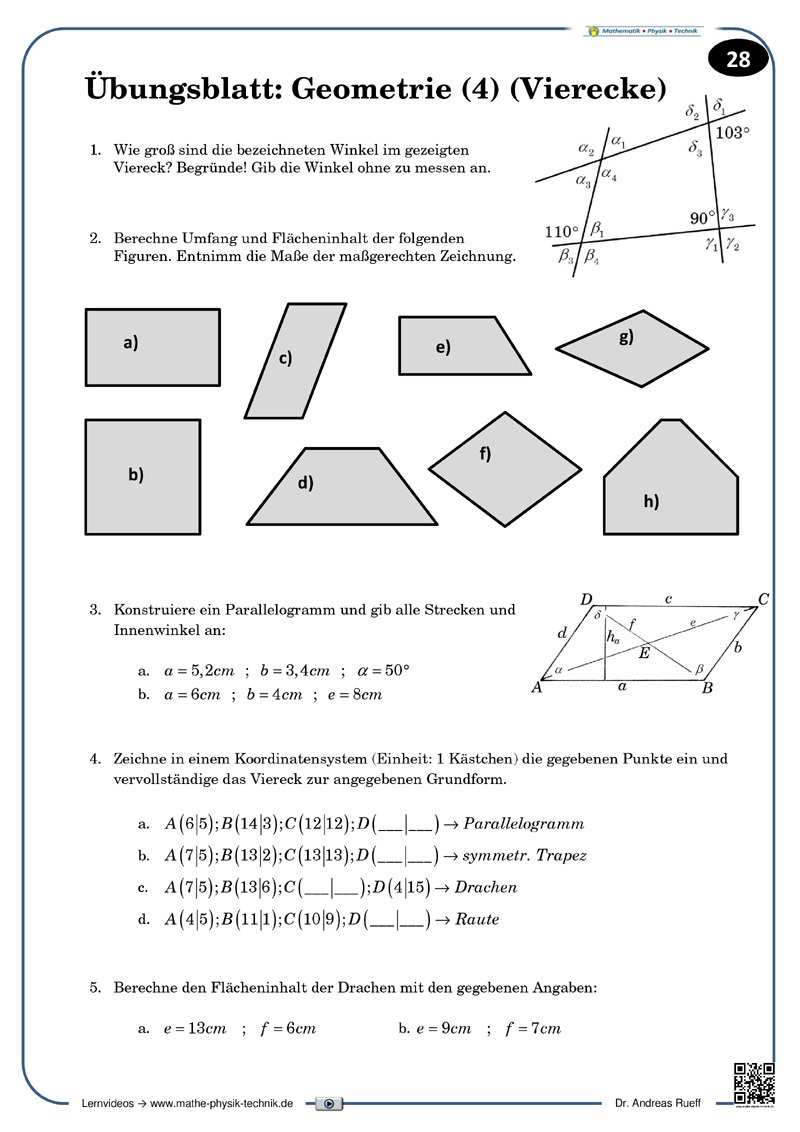
Winkelsumme in Dreieck und Viereck
Die Winkelsumme in Dreieck und Viereck wird anschaulich dargestellt.
........................................................................................................

Geometrie: [1:38]
Grundkonstruktionen - Das gleichseitige Dreieck
........................................................................................................

Geometrie: Dreiecke [7:06]
Dreiecke → Inkreis - Umkreis - Schwerpunkt
Die Konstruktion von Inkreis, Umkreis und Schwerpunkt eines Dreiecks wird vorgeführt. Es wird dabei Bezug genommen auf die Grundkonstruktionen (vgl. verlinkte Videos).
........................................................................................................

Geometrie: Satz des Thales [3:57]
Rechtwinklige Dreiecke konstruieren, Beweis
Die Konstruktion rechtwinkliger Dreiecke auf Grundlage des Satzes von Thales wird demonstriert und anschließend der Satz anschaulich bewiesen.
........................................................................................................

Geometrie: Dreiecke [2:58]
Dreiecke konstruieren ( 1. Fall: SSS )
Die Konstruktion von Dreiecken wird anhand eines Beispiels vorgeführt - hier der erste Fall: SSS (Drei Seiten sind gegeben) - Kongruenzsätze
........................................................................................................

Geometrie: Dreiecke [2:58]
Dreiecke konstruieren ( 2. Fall: SWS )
Die Konstruktion von Dreiecken wird anhand eines Beispiels vorgeführt - hier der zweite Fall: SWS (Zwei Seiten und der eingeschlossene Winkel sind gegeben) - Kongruenzsätze
........................................................................................................

Geometrie: Dreiecke [3:04]
Dreiecke konstruieren ( 3. Fall: WSW )
Die Konstruktion von Dreiecken wird anhand eines Beispiels vorgeführt - hier der dritte Fall: WSW - Kongruenzsätze
........................................................................................................

Geometrie: Dreiecke [2:49]
Dreiecke konstruieren ( 4. Fall: SWW )
Die Konstruktion von Dreiecken wird anhand eines Beispiels vorgeführt - hier der vierte Fall: SWW - Kongruenzsätze
........................................................................................................

Geometrie: Dreiecke [4:10]
Dreiecke konstruieren ( 5. Fall: SSW )
Die Konstruktion von Dreiecken wird anhand eines Beispiels vorgeführt - hier der fünfte Fall: SSW - Kongruenzsätze
........................................................................................................

Geometrie: Dreiecke [3:47]
Flächenberechnung am Dreieck
Gezeigt wird die Berechnung der Fläche eines allgemeinen Dreiecks.
........................................................................................................

Geometrie: Der Satz des Pythagoras [7:11]
Motivation, Beweis, Anwendung
Der Satz des Pythagoras wird bewiesen. Die dadurch möglichen Dreiecksberechnungen als Grundlage für weiterführende Berechnungen werden demonstriert. Abschließend wird in einem einfachen Beispiel eine Anwendung des S.d.P. gezeigt.
........................................................................................................

Geometrie: Euklid: Höhensatz [3:20]
Anschauliche Herleitung
Anschaulich beschrieben wird der Beweis des Höhensatzes des Euklid.
........................................................................................................

Geometrie: Euklid: Kathetensatz [4:37]
Anschauliche Herleitung
Anschaulich beschrieben wird der Beweis des Kathetensatzes des Euklid.


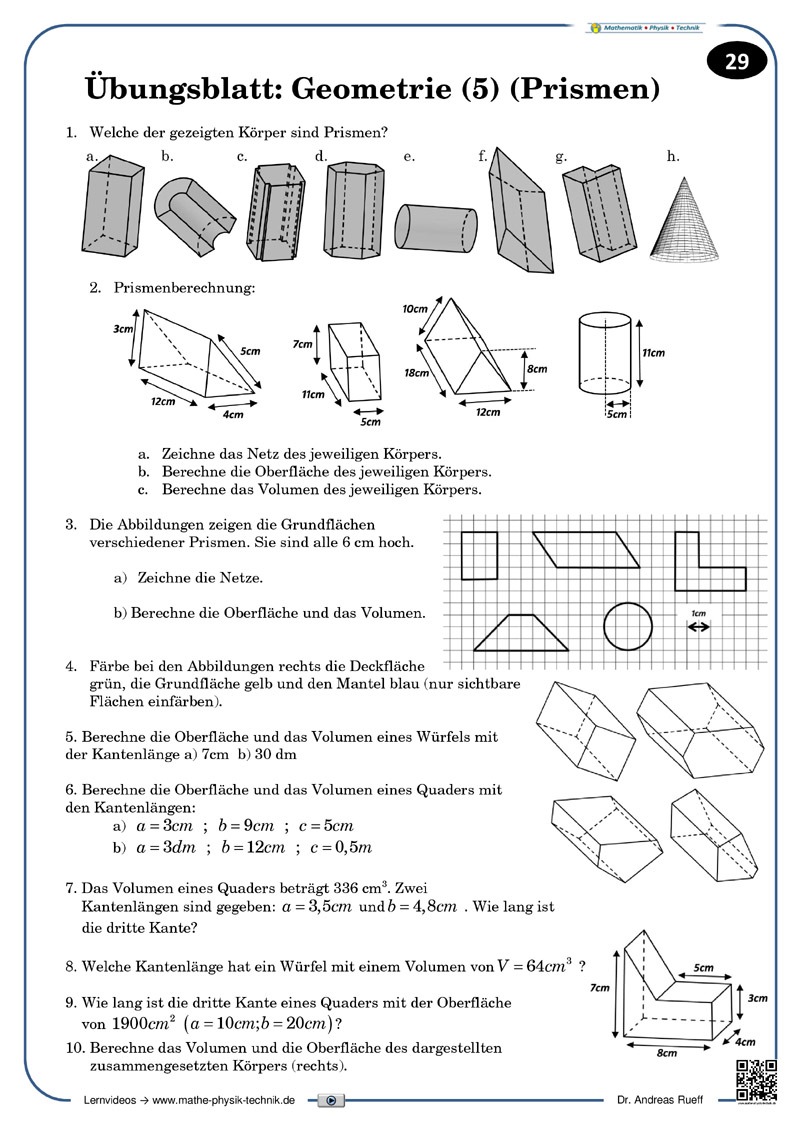
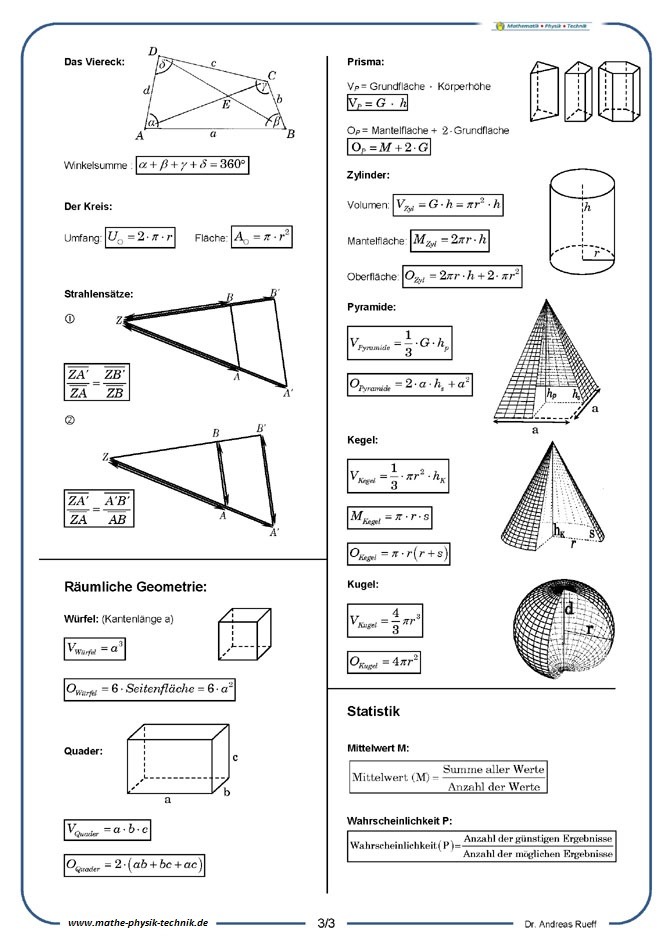
Geometrie - Körpernetze (Abwicklungen): [3:16]
Beispiele: Quader und Würfel
Die Abwicklung eines Körpers zum Erhalt des Körpernetzes wird am Beispiel eines Quaders vorgeführt. Allgemeine Grundlagen zu Netzen werden zusammengefasst.
........................................................................................................

Geometrie: Parallelogramm und Raute [4:17]
Flächenberechnung an Parallelogramm und Raute
Die Berechnung der Fläche eines Parallelogramms (bzw. einer Raute) wird durch einfache Symmetrieüberlegungen gezeigt.
........................................................................................................

Geometrie: Trapez [3:25]
Flächenberechnung am Trapez
Die Berechnung der Fläche eines Trapezes wird durch einfache Symmetrieüberlegungen gezeigt.


Geometrie - Flächeneinheiten: [6:14]
Flächeneinheiten und Umrechnungen
Die Umrechnung von Flächeneinheiten wird vorgeführt. Veranschaulicht wird dabei die Umrechnungszahl 100. Flächeneinheiten für große und gleine Flächeninhalte werden eingeführt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Geometrie - Volumenberechnung (1): [5:45]
Volumenformel für den Quader /
Volumeneinheit: Kubikzentimeter
Die Berechnung des Volumens eines Quaders wird anschaulich dargestellt. Zwei verschiedene Quader werden mit Kubikzentimeterwürfeln aufgefüllt, dadurch das Volumen bestimmt und die Einheit "Kubikzentimeter" dadurch eingeführt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
........................................................................................................

Geometrie - Volumenberechnung (2): [6:20]
Volumeneinheiten und Umrechnungen
Die zur Angabe des Volumens eines Quaders notwendigen Einheiten (Kubikzentimeter, Kubikdezimeter, etc.) und deren Zusammenhänge werden anschaulich dargestellt.
 Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Experimentelle Verfahren zur Volumenbestimmung werden in den Videobeiträgen zum Differenzenverfahren und zum Überlaufverfahren gezeigt.
........................................................................................................

Geometrie - Schrägbilder: [6:47]
Gezeigt wird die Konstruktion von Schrägbildern - Mathematik, Mittelstufe. Dabei werden die grundlegenden Regeln eingeführt und beschreiben. Anschließend werden zwei Beispiele mit
allen notwendigen Einzelheiten vorgeführt: 1) Ein Quader und 2) ein Dreiecksprisma.
Diese Darstellungsart wird auch als Kabinett-Ansicht bezeichnet.
........................................................................................................

Geometrie - Körpernetze (Abwicklungen): [3:16]
Beispiele: Quader und Würfel
Die Abwicklung eines Körpers zum Erhalt des Körpernetzes wird am Beispiel eines Quaders vorgeführt. Allgemeine Grundlagen zu Netzen werden zusammengefasst.
........................................................................................................

Geometrie: Der Zylinder (1) [8:52]
Die Oberflächenformel
Die Oberflächenformel für den Zylinder wird anschaulich hergeleitet. Anschließend werden die Ergebnisse in einer Übersicht zusammengefasst und noch ein Beispiel vorgerechnet.
........................................................................................................

Geometrie: Der Zylinder (2) [4:21]
Die Volumenformel
Die Volumenformel eines Zylinders wird anschaulich hergeleitet. Anschließend werden die Ergebnisse zusammengefasst und ein Beispiel vorgerechnet.


Gleichungen: Binomische Formeln (1) [2:49]
Teil 1 - Erste binomische Formel
Anschaulich hergeleitet werden die binomischen Gleichungen durch geometrische Überlegungen. [ Binome, Binom ]
........................................................................................................
 Die Arbeitsblätter auf dieser Seite sind lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Die Arbeitsblätter auf dieser Seite sind lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Übersicht der Rechen-Tools im → Lern-Archiv
und auf den → Themenseiten
1. Mathematik
Mini-Taschenrechner
Teilermenge / Primfaktorzerlegung
Potenzen
Berechnungen mit zwei Bruechen
Umwandlung: Bruch nach % oder Dezimal
Umwandlung: Prozent in Dezimalbruch und Bruch
Umwandlung: Dezimalbruch in Prozent und Bruch
Dezimalzahlen runden
Grundwert aus Prozentwert und Prozentsatz
Prozentsatz aus Grundwert und Prozentwert
Prozentwert aus Grundwert und Prozentsatz
Jahreszinsen
Monatszinsen
Tageszinsen
Zinseszinsen
Potenzen
Wurzeln berechnen
Logarithmus
Gleichungen
Gleichungen loesen (allg.)
Quadratische Gleichungen loesen
Gleichungssystem mit zwei Unbekannten
Gleichnungsystem mit drei Unbekannten
Funktionen
Wertetabelle erstellen
Funktionen darstellen (allg.)
Lineare Funktionen darstellen
Quadratische Funktionen darstellen
Proportionale Zuordnungen (Dreisatz)
Antiproportionale Zuordnungen
Exponentielles Wachstum/Abnahme (1)
Exponentielles Wachstum/Abnahme (2)
Exponentielles Wachstum/Abnahme (3)
Exponentielles Wachstum/Abnahme (4)
Exponentielles Wachstum/Abnahme (5)
Exponentielles Wachstum/Abnahme (6)
Trigonometrische Funktionen darstellen
Geometrie
Berechnungen am Zylinder
Berechnungen am Kegel
Berechnungen an der Kugel
Berechnungen am allgemeinen Dreieck (SSS)
Berechnungen am allgemeinen Dreieck (SWS)
Berechnungen am allgemeinen Dreieck (SWW)
Berechnungen am allgemeinen Dreieck (WSW)
Berechnungen - Pythagoras
Berechnungen am Kreis
Berechnungen an der Pyramide
Trigonometrie
Grad / Bogenmass
Trigonometrische Funktionen
Trigonometrische Umkehrfunktionen
Analysis
Folgen & Reihen
Polynomdivision berechnen
Taylorreihe
Riemannsche Summen
Grenzwerte berechnen
Berechnung der Ableitungsfunktion
Extremstellen berechnen
Berechnung des bestimmten Integrals
Berechnung des unbestimmten Integrals
Analytische Geometrie
Betrag eines Vektors
Abstandsformel im Raum R^3
Winkel zwischen zwei Vektoren
Addition von Vektoren
Subtraktion von Vektoren
Skalar-Multiplikation von Vektoren
Skalarprodukt von Vektoren
Kreuzprodukt von Vektoren
Umwandlung: Normalenform in Koordinatenform
Normalenvektor berechnen
Berechnung: Abstand Punkt - Ebene
Stochastik
Bernoulli / Binomialverteilung
Formel von Bernoulli B(n;p;k)
Kombinatorik - nPr
Kombinatorik - Binomialkoeffizienten (nCr)
Formel von Bernoulli / Binomialverteilung B(n;p;k)
Kumulierte Binomialverteilung F(n;p;k)
Normalverteilung zeichnen
3D-Funktionen darstellen
Komplexe Zahlen
Rechnen mit komplexen Zahlen (C)
Umwandeln: Polarform einer komplexen Zahl
2. Physik/Technik
Vorsaetze fuer Masseinheiten
Umrechnen: Laengeneinheiten
Umrechnen: Flaecheneinheiten
Umrechnen: Volumeneinheiten
Umrechnen: Zeiteinheiten
Umrechnung: Masseeinheiten
Umrechnen: Druckeinheiten
Umrechnungen: Dichteeinheiten
Umrechnung: Temperatureinheiten
Umrechnung: Leistungseinheiten
Umrechnung: Energieeinheiten
Zahlensysteme umrechnen
Boolesche Algebra (1) - Wahrheitstabellen
Boolesche Algebra (2)
Logische Schaltungen
Sichtbarer Sternenhimmel nach Ort und Zeit
Himmelsausschnitt und Sternzeit
Naechste Finsternisse
Mondphase
Planeten- und Mondpositionen
Aktuelle Daten zu Himmelskoerpern
Brechung an transparenten Medien (Snellius)
Bildentstehung bei der Linse
Brechung am Prisma
Konkavspiegel (Hohlspiegel)
Konvexspiegel (Woelbspiegel)
Subtraktive Farbmischung
Energieverbrauch - Statistik
Energiegewinnung - Statistiken
Periodensystem der Elemente
Eigenschaften der Elemente
Spezifische Aktivitaet
Halbertszeit von Isotopen
Elementeigenschaften
Isotope
Zerfallsreihen
Standorte von Kernkraftwerken
Hohe Bauwerke
Brücken
Motorisierte Luftfahrt
Schnelle Flugzeuge
QR-Code Generator
Produktlinks (amazon.de):

Aus dieser Seite sind Online-Übungen eingebunden. Diese sind bei www.learningapps.org erstellt worden, es kann sich auch teilweise um Apps von externen Erstellern handeln.