Mathematik - Übungsblätter (4)
( Nr. 31 - 40)
Mathematik:
Übungsheft zu den Grundlagen für die Mittelstufe
→ Übungsblätter (ISBN 9783744869126)
→ Lösungsheft (ISBN 9783744869607)
Hinweis:
Für den Unterricht ist die Anschaffung der Skripte und Bücher für meine Schüler nicht notwendig und nicht empfohlen! Die Übungsblätter werden bei Bedarf bearbeitet und notwendige Materialien
ggf. kopiert.
Gleichungen: Binomische Formeln (1) [2:49]
Teil 1 - Erste binomische Formel
Anschaulich hergeleitet werden die binomischen Gleichungen durch geometrische Überlegungen. [ Binome, Binom ]
........................................................................................................
Gleichungen: Binomische Formeln (2) [3:48]
Teil 2 - Zweite binomische Formel
Anschaulich hergeleitet werden die binomischen Gleichungen durch geometrische Überlegungen. [ Binome, Binom ]
........................................................................................................
Gleichungen: Binomische Formeln (3) [3:22]
Teil 3 - Dritte binomische Formel
Anschaulich hergeleitet werden die binomischen Gleichungen durch geometrische Überlegungen. [ Binome, Binom ]
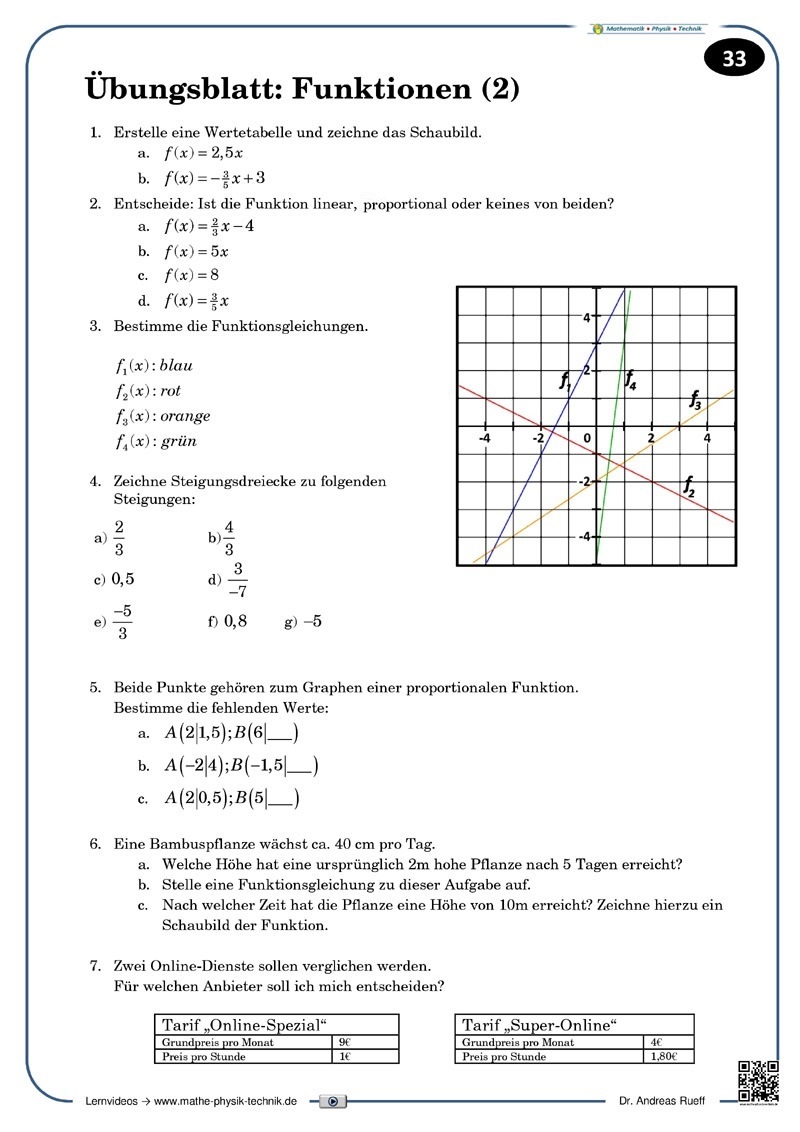
Funktionen: Lineare Funktionen (1) [6:07]
Veranschaulicht wird der Funktionsbegriff und wie über eine Wertetabelle allgemein eine Funktion in einem Diagramm mithilfe der Funktionsgleichung dargestellt werden kann.
........................................................................................................
Funktionen: Lineare Funktionen (2) [5:52]
Veranschaulicht werden lineare Funktionen die durch den Ursprung verlaufen (y = m ∙ x). An Beispielen werden Funktionsgleichungen systematisch verändert und so der Zugang zu linearen Funktionsgraphen erreicht.
........................................................................................................
Funktionen: Lineare Funktionen (3) [5:56]
Veranschaulicht werden allgemeine lineare
Funktionen (y = m ∙ x + n).
........................................................................................................
Funktionen: Lineare Funktionen (4) [5:41]
Lineare Funktionen im Koordinatensystem darstellen
An Beispielen wird demonstriert wie lineare Funktionen nach Vorgabe der Funktionsgleichung ins Koordinatensystem eingezeichnet werden.
........................................................................................................
Funktionen: Lineare Funktionen (5) [7:51]
Das Steigungsdreieck (1)
An Beispielen wird die Handhabung des Steigungsdreiecks bei linearen Funktionen demonstriert. Die Steigung ist in den Beispielen jew. ganzzahlig. Nach Vorgabe der Funktionsgleichung werden die Funktionen ins Koordinatensystem eingezeichnet werden.
........................................................................................................
Funktionen: Lineare Funktionen (6) [6:18]
Das Steigungsdreieck (2)
An Beispielen wird die Handhabung des Steigungsdreiecks bei linearen Funktionen demonstriert. Die Steigung ist in den Beispielen jew. eine Bruchzahl. Nach Vorgabe der Funktionsgleichung werden die Funktionen ins Koordinatensystem eingezeichnet werden.
Geometrie: Zentrische Streckung [3:55]
Anschaulich vorgeführt wird am Beispiel eines Dreiecks die zentrische Streckung mit Streckfaktor 2,5.
........................................................................................................
Geometrie: Ähnlichkeit und Kongruenz [8:55]
Die Begriffe "Ähnlichkeit" und "Kongruenz" werden an einem Beispiel erklärt. Dabei wird auch unterschieden zwischen der gleichsinnigen und ungleichsinnigen Ähnlichkeit bzw. Kongruenz.
........................................................................................................
Geometrie: Strahlensätze [8:03]
Motivation, Beweis, Anwendung
Die Strahlensätze werden detailliert und schrittweise hergeleitet und anschließend ein Beispiel zur Anwendung gezeigt und vorgerechnet.
Geometrie: Der Satz des Pythagoras [7:11]
Motivation, Beweis, Anwendung
Der Satz des Pythagoras wird bewiesen. Die dadurch möglichen Dreiecksberechnungen als Grundlage für weiterführende Berechnungen werden demonstriert. Abschließend wird in einem einfachen Beispiel eine Anwendung des S.d.P. gezeigt.
........................................................................................................
Geometrie: Euklid: Höhensatz [3:20]
Anschauliche Herleitung
Anschaulich beschrieben wird der Beweis des Höhensatzes des Euklid.
........................................................................................................
Geometrie: Euklid: Kathetensatz [4:37]
Anschauliche Herleitung
Anschaulich beschrieben wird der Beweis des Kathetensatzes des Euklid.
Abonnieren:
Geometrie: Der Kreis (1) [6:17]
Bestimmung des Kreisumfangs - Kreiszahl π (Pi) -
Beispielrechnungen
Die Formel zur Berechnung des Kreisumfangs wird anschaulich hergeleitet und die Kreiszahl Pi eingeführt. Anschließend werden zwei Anwendungsbeispiele vorgerechnet.
........................................................................................................
Geometrie: Der Kreis (2) [5:25]
Bestimmung der Kreisfläche: Herleitung und Beispielrechnungen
Die Formel zur Berechnung der Kreisfläche wird anschaulich hergeleitet. Anschließend werden zwei Anwendungsbeispiele vorgerechnet.
........................................................................................................
Geometrie: Der Kreis (3) [5:03]
Berechnung von Kreissegmenten und Kreisbögen
Die Grundlagen zur Berechung von Kreisteilen: Kreissegmente und Kreisbögen wird anschaulich demonstriert. Anschließend werden Beispiele vorgerechnet.
Wurzeln (Radizieren) / Intervallschachtelung [8:22]
Es werden zunächst grundlegende Zusammenhänge und Begriffe zum Thema Wurzeln erklärt. Anschließend wird an einem Beispiel das
Verfahren der Intervallschachtelung vorgeführt.
........................................................................................................
Wurzeln: Die n-te Wurzel [6:20]
Es werden Grundlagen zum Wurzelziehen gezeigt. Insbesondere die Erweiterung des Wurzelbegriffs für die n-te Wurzel. An Beispielen
wird die Handhabung erarbeitet und erklärt.
Geometrie: Der Zylinder (1) [8:52]
Die Oberflächenformel
Die Oberflächenformel für den Zylinder wird anschaulich hergeleitet. Anschließend werden die Ergebnisse in einer Übersicht zusammengefasst und noch ein Beispiel vorgerechnet.
........................................................................................................
Geometrie: Der Zylinder (2) [4:21]
Die Volumenformel
Die Volumenformel eines Zylinders wird anschaulich hergeleitet. Anschließend werden die Ergebnisse zusammengefasst und ein Beispiel vorgerechnet.
........................................................................................................
Geometrie: Die Pyramide [3:42]
Die Volumenformel
Anschaulich wird die Herleitung der Volumenformel für die Pyramide gezeigt.
........................................................................................................
Geometrie: Die Pyramide [3:11]
Die Oberfläche (1)
Beschrieben und veranschaulicht wird die Berechnung der Oberfläche einer Pyramide.
........................................................................................................
Geometrie: Die Pyramide [3:39]
Die Oberfläche (2) - Zusammenhang der Größen
Beschrieben und veranschaulicht werden die Zusammenhänge der charakteristischen Größen einer Pyramide zur Oberflächenberechnung.
........................................................................................................
Geometrie: Die Pyramide [3:21]
Abwicklung der Oberfläche - Das Netz der
Pyramide
........................................................................................................
Geometrie - Kegel - Die Oberfläche [8:13]
Oberflächenformel für den Kreiskegel
Die Formel zur Berechnung der Oberfläche eines Kegels wird anschaulich hergeleitet. Anschließend werden die Ergebnisse zusammengefasst und ein Beispiel vorgerechnet.
...............................................................
Geometrie - Kegel - Volumenformel [4:45]
Volumenformel für den Kreiskegel
Herleitung der Volumenformel für den Kreiskegel, ausgegangen wird hier von der Volumenformel der Pyramide. Anschließend wird noch ein Beispiel vorgerechnet.
...............................................................
Geometrie - Kugel - Oberfläche [4:06]
Herleitung der Oberflächenformel für eine Kugel
Anschaulich gezeigt wird die Herleitung der Oberflächenformel für die Kugel.
...............................................................
Geometrie - Kugel - Oberfläche [4:06]
Herleitung der Oberflächenformel für eine Kugel
Anschaulich gezeigt wird die Herleitung der Oberflächenformel für die Kugel.
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise
(manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise
(manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
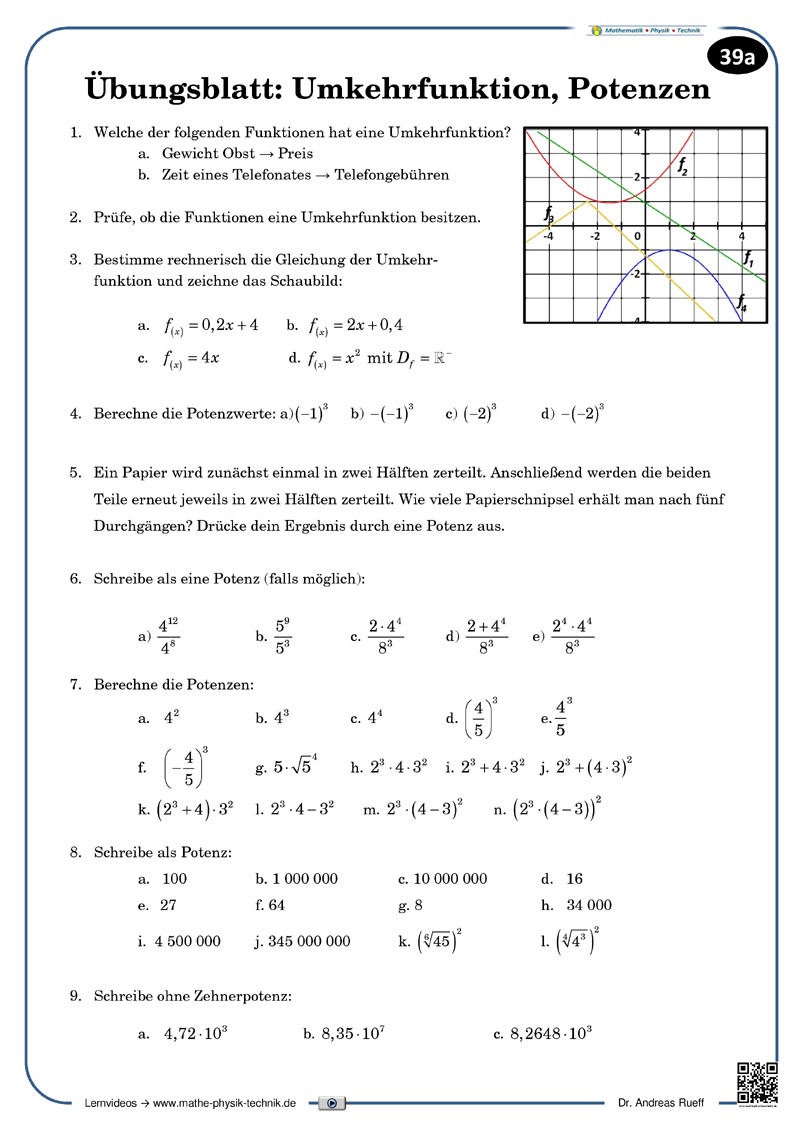
Potenzen (1): 1. und 2. Potenzsatz [7:56]
Multiplikation von Potenzen mit gleichen Basen
Daraus leiten sich der ersten und der zweite Potenzsatz ab. Es werden anschließend Beispiele gezeigt.
........................................................................................................
Potenzen (2): 3. und 4. Potenzsatz [7:30]
Multiplikation von Potenzen mit gleichen Exponenten
Daraus leiten sich der dritte und der vierte Potenzsatz ab. Es werden anschließend Beispiele gezeigt.
........................................................................................................
Potenzen (3): Addition und Subtraktion [6:57]
Addition und Subtraktion von Potenzen
Vereinfachungen ergeben sich hier nur bei gleicher Basis und gleichem Exponent. Es werden anschließend Beispiele gezeigt.
........................................................................................................
Potenzen (4): 5. Potenzsatz [5:41]
Potenzieren von Potenzen
Daraus leitet sich der fünfte Potenzsatz ab. Es werden anschließend Beispiele gezeigt.
........................................................................................................
Potenzen (5): Ganzzahlige Exponenten [8:14]
Erweiterung auf ganzzahlige Exponenten
Hierbei werden logische Folgerungen aus dem zweiten Potenzsatz vorgeführt und die Bedeutung von negativen Exponenten erklärt. Es werden anschließend Beispiele gezeigt.
........................................................................................................
Potenzen (6): Rationale Exponenten [8:19]
Im sechsten Teil der Videoreiche wird die Erweiterung auf rationale Exponenten gezeigt. Hierbei werden logische Folgerungen aus dem
fünften Potenzsatz vorgeführt und die Bedeutung von Buchzahlen im Exponenten erklärt. Es werden anschließend Beispiele gezeigt.
........................................................................................................
Funktionen: Potenzfunktionen [6:27]
Eigenschaften von Potenzfunktionen
Die grundlegenden Eigenschaften von Potenzfunktionen werden beschrieben.
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise
(manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise
(manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise
(manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise
(manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
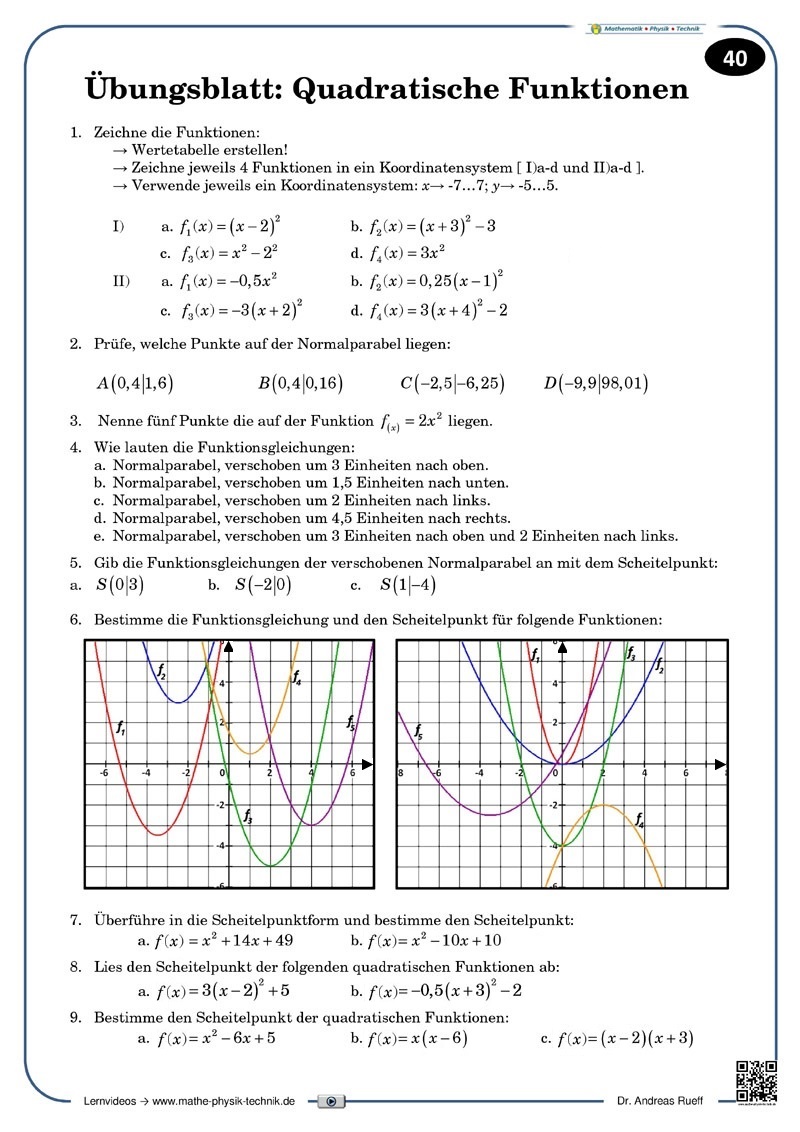
Funktionen: Quadratische Funktionen (1) [4:18]
Quadratische Gleichungen vom Typ y=x2+c.
Ausgehend von der Normalparabel werden Verschiebungen in y-Richtung veranschaulicht und begründet.
Vorausgesetzte Grundlagen für die Videos
zu quadratischen Funktionen sind: Lineare Funktionen
........................................................................................................
Funktionen: Quadratische Funktionen (2) [3:35]
Quadratische Gleichungen vom Typ y=(x+b)2+c.
Ausgehend von der Normalparabel werden Verschiebungen in x-Richtung veranschaulicht und begründet. Anschließend werden zusammengesetzte Verschiebungen an Beispielen gezeigt.
........................................................................................................
Funktionen: Quadratische Funktionen (3) [6:19]
Quadratische Gleichungen vom Typ y=a(x+b)2+c.
Ausgehend von der Normalparabel werden Verschiebungen gestauchte und gestreckte Parabeln veranschaulicht und begründet.
Die Arbeitsblätter auf dieser Seite sind lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Übersicht der Rechen-Tools im → Lern-Archiv
und auf den → Themenseiten
1. Mathematik
Mini-Taschenrechner
Teilermenge / Primfaktorzerlegung
Potenzen
Berechnungen mit zwei Bruechen
Umwandlung: Bruch nach % oder Dezimal
Umwandlung: Prozent in Dezimalbruch und Bruch
Umwandlung: Dezimalbruch in Prozent und Bruch
Dezimalzahlen runden
Grundwert aus Prozentwert und Prozentsatz
Prozentsatz aus Grundwert und Prozentwert
Prozentwert aus Grundwert und Prozentsatz
Jahreszinsen
Monatszinsen
Tageszinsen
Zinseszinsen
Potenzen
Wurzeln berechnen
Logarithmus
Gleichungen
Gleichungen loesen (allg.)
Quadratische Gleichungen loesen
Gleichungssystem mit zwei Unbekannten
Gleichnungsystem mit drei Unbekannten
Funktionen
Wertetabelle erstellen
Funktionen darstellen (allg.)
Lineare Funktionen darstellen
Quadratische Funktionen darstellen
Proportionale Zuordnungen (Dreisatz)
Antiproportionale Zuordnungen
Exponentielles Wachstum/Abnahme (1)
Exponentielles Wachstum/Abnahme (2)
Exponentielles Wachstum/Abnahme (3)
Exponentielles Wachstum/Abnahme (4)
Exponentielles Wachstum/Abnahme (5)
Exponentielles Wachstum/Abnahme (6)
Trigonometrische Funktionen darstellen
Geometrie
Berechnungen am Zylinder
Berechnungen am Kegel
Berechnungen an der Kugel
Berechnungen am allgemeinen Dreieck (SSS)
Berechnungen am allgemeinen Dreieck (SWS)
Berechnungen am allgemeinen Dreieck (SWW)
Berechnungen am allgemeinen Dreieck (WSW)
Berechnungen - Pythagoras
Berechnungen am Kreis
Berechnungen an der Pyramide
Trigonometrie
Grad / Bogenmass
Trigonometrische Funktionen
Trigonometrische Umkehrfunktionen
Analysis
Folgen & Reihen
Polynomdivision berechnen
Taylorreihe
Riemannsche Summen
Grenzwerte berechnen
Berechnung der Ableitungsfunktion
Extremstellen berechnen
Berechnung des bestimmten Integrals
Berechnung des unbestimmten Integrals
Analytische Geometrie
Betrag eines Vektors
Abstandsformel im Raum R^3
Winkel zwischen zwei Vektoren
Addition von Vektoren
Subtraktion von Vektoren
Skalar-Multiplikation von Vektoren
Skalarprodukt von Vektoren
Kreuzprodukt von Vektoren
Umwandlung: Normalenform in Koordinatenform
Normalenvektor berechnen
Berechnung: Abstand Punkt - Ebene
Stochastik
Bernoulli / Binomialverteilung
Formel von Bernoulli B(n;p;k)
Kombinatorik - nPr
Kombinatorik - Binomialkoeffizienten (nCr)
Formel von Bernoulli / Binomialverteilung B(n;p;k)
Kumulierte Binomialverteilung F(n;p;k)
Normalverteilung zeichnen
3D-Funktionen darstellen
Komplexe Zahlen
Rechnen mit komplexen Zahlen (C)
Umwandeln: Polarform einer komplexen Zahl
2. Physik/Technik
Vorsaetze fuer Masseinheiten
Umrechnen: Laengeneinheiten
Umrechnen: Flaecheneinheiten
Umrechnen: Volumeneinheiten
Umrechnen: Zeiteinheiten
Umrechnung: Masseeinheiten
Umrechnen: Druckeinheiten
Umrechnungen: Dichteeinheiten
Umrechnung: Temperatureinheiten
Umrechnung: Leistungseinheiten
Umrechnung: Energieeinheiten
Zahlensysteme umrechnen
Boolesche Algebra (1) - Wahrheitstabellen
Boolesche Algebra (2)
Logische Schaltungen
Sichtbarer Sternenhimmel nach Ort und Zeit
Himmelsausschnitt und Sternzeit
Naechste Finsternisse
Mondphase
Planeten- und Mondpositionen
Aktuelle Daten zu Himmelskoerpern
Brechung an transparenten Medien (Snellius)
Bildentstehung bei der Linse
Brechung am Prisma
Konkavspiegel (Hohlspiegel)
Konvexspiegel (Woelbspiegel)
Subtraktive Farbmischung
Energieverbrauch - Statistik
Energiegewinnung - Statistiken
Periodensystem der Elemente
Eigenschaften der Elemente
Spezifische Aktivitaet
Halbertszeit von Isotopen
Elementeigenschaften
Isotope
Zerfallsreihen
Standorte von Kernkraftwerken
Hohe Bauwerke
Brücken
Motorisierte Luftfahrt
Schnelle Flugzeuge
QR-Code Generator
Produktlinks (amazon.de):
