
Mechanik (3)
Hier findest du alle Inhalte zur Unterrichtseinheit.
Inhalt - Mechanik
Körper und ihre Eigenschaften
Körper und Stoffe
Unterscheide zwischen Körpern und Stoffen
Größen und Einheiten
Kräfte und ihre Wirkung
Kräfte darstellen und messen
Kräfte werden gemessen – Aufgaben
Die Federkonstante
Schwere Masse / Träge Masse
Größenbereiche – Die Masse
Masseeinheiten
Die Grundeinheit ist das Kilogramm (1kg)
Das Volumen
Größenbereiche – Das Volumen
Die Dichte eines Körpers
Aufgaben zur Dichte
Der Auftrieb im Wasser
Schwimmen – schweben - sinken
Der Flaschentaucher
→ Teil 2:
Mehrere Kräfte wirken gleichzeitig
Das Kräfteparallelogramm – Übung
Flächenbelastung und Druck
Der Druck in Flüssigkeiten
Reibung
Drehmoment und Hebel
Kräfte umleiten – Seil, Stange, Rollen
Die Arbeit
Die Energie
Die mechanische Leistung
Teil 3 (Kinematik):
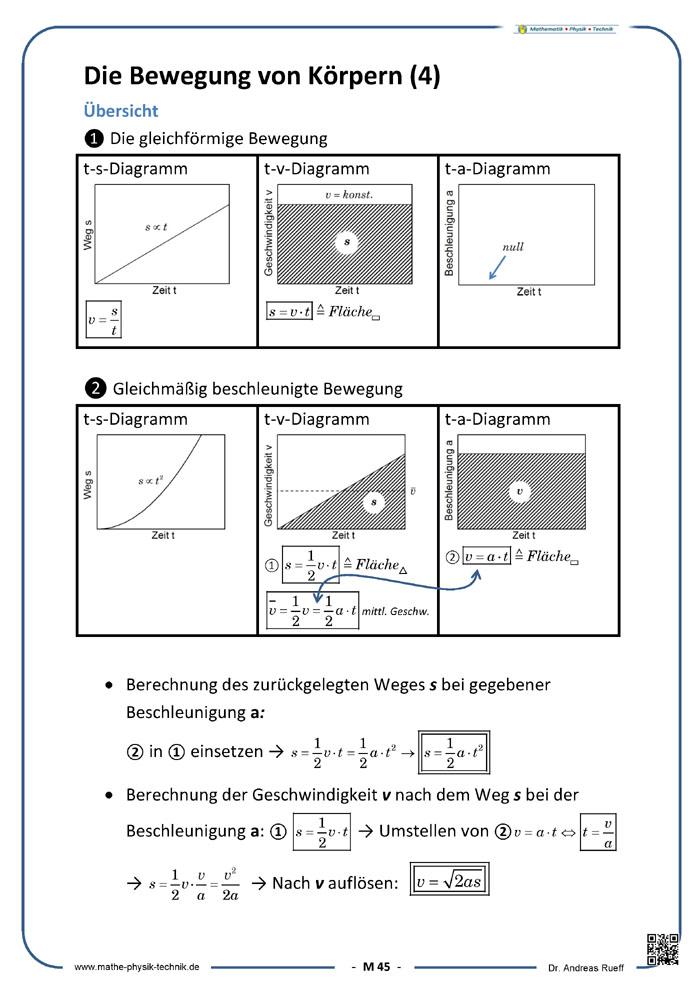
Die Bewegung von Körpern
Vorüberlegungen
Die Geschwindigkeit
Die beschleunigte Bewegung
Übersicht
Newton'sches Kraftgesetz
Impuls und Kraftstoß
Allgemeine Hinweise zu den Themenseiten
Die hier angebotenen Themenseiten fassen die grundlegenden Inhalte, Informationen und Hefteinträge zu den Unterrichtsinhalten von verschiedenen Themenbereichen der Fächer Mathematik, Physik und dem Wahlpflichtfach MINT/Technik zusammen. Diese sind online, kostenlos und ohne Registrierung verfügbar und sollen zur besseren Selbstorganisation der Schüler beitragen.
Die im Internet bereitgestellten Materialien bieten aber auch noch zusätzliche Möglichkeiten: Sie sollen den Schülern einen Leitfaden zur Vorbereitung auf Kursarbeiten, aber auch bei Fehlstunden zur Nacharbeit der versäumten Unterrichtsinhalte dienen und weiterhin den Eltern die Möglichkeit zur Unterstützung bei den unterrichtsbegleitenden Hilfestellungen geben. Die Zusammenfassungen zu den Unterrichtsinhalten auf den Themenseiten werden dabei jeweils ergänzt durch Lernvideos, Infotexten, Aufgaben, Bildergalerien und interaktiven Tools. Diese sollen dabei helfen selbstständig eigene Ergebnisse zu überprüfen oder zusätzliche Informationen zu den Inhalten erhalten. Bei den Lernvideos handelt es sich teilweise um die YouTube-Video des YT-Kanals Mathe-Physik-Technik. Weiterhin sind bei den einzelnen Folien zusätzliche Videovorschläge von anderen YouTube-Kanälen zugeordnet. Der jeweilige Link leitet dann ggf. direkt auf die YouTube-Video-Seite weiter.
Bei den klassischen physikalischen Themenbereichen sind die jeweiligen Folien für den digitalen Unterricht weitestgehend angepasst und optimiert worden. Insbesondere durch die Corona-Krise rückt der digitale und eigenverantwortliche Unterricht immer mehr in den Fokus. Zu den einzelnen Folien sind deshalb jeweils passende Videos zu den Inhalten zugeordnet und zu vielen Folien auch passende Aufgaben eingearbeitet worden. Dadurch sind die Themenbereiche in Teilabschnitten strukturiert und für die Arbeit mit Wochenplänen optimiert worden. Sie ermöglichen den Schülern so die selbstständige Arbeit daheim und geben jedem Schüler die Möglichkeit die Lernziele auch unter den gegebenen Umständen bestmöglich zu erreichen. Dabei können Schüler dann sogar die positiven Seiten des digitalen Unterrichts (Eigenes Lerntempo festlegen, optimale Anpassung von Lernzeit und Zeitpunkt an den eigenen Biorhythmus zum effizienten Lernen, etc.) für sich besonders gut nutzen.
Siehe hierzu auch: → Konzept - mathe-physik-technik.de
Skript → Publikationen
Kinematik

Infotext - Die Bewegung von Körpern (1) - Bezugssysteme, Massenpunkte
Bezugssysteme
Durch das Bezugssystem wird ein reales physikalisches System auf die denkbar einfachste Grundlage an Daten reduziert. Zur Beschreibung der Bewegung eines Autos ist beispielsweise seine Farbe oder der Hersteller des Autos völlig unwichtig. Ein Bezugssystem ist in der Physik ein gedachtes raum-zeitliches Gebilde, das erforderlich ist, um das Verhalten ortsabhängiger Größen eindeutig und vollständig zu beschreiben. Insbesondere können die Lage und Bewegung von physikalischen Körpern nur relativ zu einem Bezugssystem angegeben werden.
Ein Bezugssystem wird definiert, indem man einen Bezugspunkt wählt und die Raumrichtungen festlegt, sowie einen physikalischen Prozess für die Zeitmessung bestimmt. Dadurch ist zunächst festgelegt, was unter „Ruhe“ und „Bewegung“ jeweils zu verstehen ist. Zudem ermöglicht dies, ein Koordinatensystem einzuführen, mit dessen Hilfe physikalische Ereignisse durch Angabe ihrer raum-zeitlichen Koordinaten mathematisch beschrieben werden können. Durch eine geschickte Wahl des Koordinatensystems kann die mathematische Beschreibung eines physikalischen Vorgangs erheblich erleichtert werden!
Wenn Beobachter von verschiedenen Bezugssystemen ausgehen, können sie zu einem physikalischen Vorgang verschiedene Beschreibungen geben, die dennoch alle zutreffen, wenn man ihr jeweiliges Bezugssystem berücksichtigt. Zum Beispiel könnte ein Autofahrer zu Recht behaupten, dass ihm ein Baum entgegenkommt, während ein am Straßenrand stehender Beobachter, ebenfalls zu Recht, den Vorgang umgekehrt sieht. In der Physik gilt, dass jedes so definierte Bezugssystem gleichberechtigt gewählt werden darf und dass es keinen grundlegenden Prozess gibt, durch den man ein bestimmtes Bezugssystem vor allen anderen auszeichnen könnte.
Massenpunkte
Als Massenpunkt oder Bezugspunkt wird häufig ein einziger Punkt eines realen Körpers gewählt, z. B. „die linke, vordere Ecke des Tisches“, „die Mitte des Bahnsteigs“ oder „das Zentrum der Sonne“. Es kann sich aber auch um einen gedachten Punkt handeln, z. B. „der gemeinsame Schwerpunkt von Erde und Mond“ oder „ein frei fallendes Bezugssystem“.
Wir betrachten als Beispiel ein Wettrennen von zwei Autos: Die Festlegung eines geeigneten Massenpunktes ist bei dem Wettrennen sehr wichtig. Dabei spielt es eine Rolle zu welchem Zeitpunkt der vorderste Punkt es jeweiligen Autos die Ziellinie überschreitet. Dieser Punkt ist deshalb eine sinnvolle Wahl für die Festlegung des Massenpunktes für das jeweilige Auto. Die Form des Körpers, seine Farbe oder auch seine Ausdehnung spielen bei der Betrachtung des Wettrennens keine Rolle.
Alle physikalischen Untersuchungen finden in dem Modell der Massenpunkte im gewählten Bezugssystem statt. Es handelt sich dabei um ein gedankliches Konstrukt. Einen Körper ohne reale Ausdehnung gibt es in unserer realen Welt natürlich nicht, trotzdem lässt sich beispielsweise seine Geschwindigkeit in dem Modell bestimmen. Die aus der Modellvorstellung abgeleiteten Ergebnisse lassen sich dann aber einfach wieder in die Realität übertragen, man erhält dadurch also Aussagen oder Vorhersagen zu dem realen physikalischen System.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
3) → Was ist ein Inertialsystem in der Physik? (EINFACH erklärt)
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
Aufgaben: Bezugssysteme und Massenpunkte
1) Vergleiche die Bilder (Abb. 1 und 2):
a. Welche Gemeinsamkeit findest du?
b. Bewerte den „Bewegungszustand“ für beide Bilder und vergleiche sie. Was bewegt sich hier eigentlich?


2) Schau dir die Abbildungen 3 und 4 an und recherchiere:
a. Bei einem 100-Meter-Lauf ist genau festgelegt, wann ein Läufer die Strecke absolviert hat. Welche Bedingung muss genau erfüllt sein, damit die Zeit für einen Läufer gestoppt
wird?
b. Beim Fußball ist genau festgelegt unter welcher Bedingung ein Tor zählt. Dafür wird heute sogar die sogenannte „Torlinientechnik“ verwendet.
Vergleiche die beiden Beispiele und finde Unterschiede und/oder Gemeinsamkeiten. Welches „Problem“ besteht hier und ist der Grund für die genauen Festlegung der „Spielregeln“?


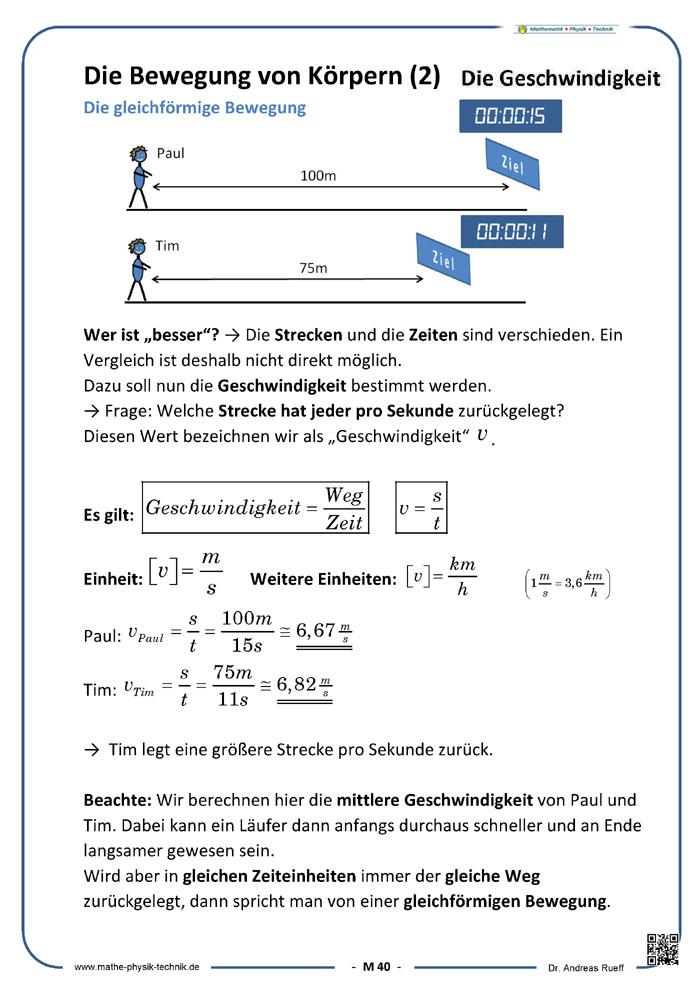
Infotext - Die Bewegung von Körpern (2) - Die Geschwindigkeit

- welche Zeit für eine bestimmte Wegstrecke benötigt wird oder
- welche Strecke in einem gegebenen Zeitintervall zurückgelegt wird.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.

Physik - Mechanik: [7:08]
Die Geschwindigkeit
Der Begriff der Geschwindigkeit wird an Beispielen erklärt. Es werden Beispiele zur Berechnung der Geschwindigkeit, der Strecke und der Zeit ausführlich vorgeführt.

Physik - Mechanik: [5:24]
Einheiten umrechnen
Diese Video zeigt die grundsätzliche Vorgehensweise zur Umrechnung von Einheiten am Beispiel der Geschwindigkeitseinheiten m/s und km/h. Weiterhin werden Beispiel gezeigt.
Zusätzliche Videos:
1) → Formel für Bewegung | alpha Lernen erklärt Physik
2) → Bewegung: die Formelumstellung üben | alpha Lernen erklärt Physik
3) → Geschwindigkeit berechnen | alpha Lernen erklärt Physik
4) → Weg-Zeit-Gesetz bei konstanter Geschwindigkeit | alpha Lernen erklärt Physik
5) → Tabellen und Diagramme | alpha Lernen erklärt Physik
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
Aufgaben: Geradlinig-gleichgörmige Bewegung
1) Berechne die Geschwindigkeiten in der
angegebenen Einheit:
a. Bei einem Marathon wird eine Strecke von 42,195 km zurückgelegt. Eine Laufzeit von 4 Stunden ist bei den Männern ein gutes Ergebnis. Berechne die Geschwindigkeit in der Einheit „Kilometer pro Stunde“.
b. Beim 800-Meter-Lauf liegen die gemessenen Zeiten bei den schnellsten Frauen bei etwa 115 Sekunden. Berechne die Geschwindigkeit in der Einheit „Meter pro Sekunde“.
c. Eine Schnecke legt in 4 Stunden eine Strecke von 12 Metern zurück. Berechne die Geschwindigkeit in der Einheit „Meter pro Stunde“.
d. Ein Delphin legt in 2,5 Stunden eine Strecke von 115 km zurück. Berechne seine Geschwindigkeit in der Einheit „Kilometer pro Stunde“.
e. Eine Feldmaus benötigt für die Strecke von 1,6 km eine
Zeit von 0,2 Stunden (= 12 Minuten). Berechne die Geschwindigkeit in der Einheit:
I) „Kilometer pro Stunde“
II) „Kilometer pro Minute“
III) „Meter pro Minute“
2) Berechnung der Strecke:
a. Ein Auto benötigt für die Entfernung von Kaiserslautern nach Berlin bei einer Geschwindigkeit von 95 Kilometern pro Stunde einen Zeitraum von 7 Stunden. Berechne die Entfernung von Kaiserslautern nach Berlin.
b. Ein Auto hat bei einer Geschwindigkeit von 75 Kilometern pro Stunde nach 4 Stunden die Entfernung von Kaiserslautern nach Nürnberg zurückgelegt. Welche Entfernung wurde dabei zurückgelegt?
c. Für die Entfernung von Hannover nach Kaiserslautern hat ein Auto bei einer Geschwindigkeit von 130 Kilometern pro Stunde eine Zeit von 3,5 Stunden benötigt. Berechne die zurückgelegte Strecke.
3) Berechnung der Zeit:
a. Ein Wanderer ist durchschnittlich mit einer Geschwindigkeit von 5 Kilometern pro Stunde unterwegs. Wie lange benötigt er für die Strecke von Kaiserslautern nach Bad Dürkheim (35 km)?
b. Die Strecke von Braunschweig nach Kaiserslautern (446 km) wurde bei einer Geschwindigkeit von 90 Kilometern pro Stunde zurückgelegt. Wie lange war das Auto unterwegs?
c. Fulda ist von Kaiserslautern etwa 217 km entfernt. Ein PKW fährt die Strecke mit einer Geschwindigkeit von 115 Kilometern pro Stunde. Wie lange ist der PKW unterwegs?
Diese App ist wurde erstellt von A. Rueff nach einer Idee von jmeuser bei
LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App ist wurde erstellt von A. Rueff nach einer Idee von jmeuser bei
LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
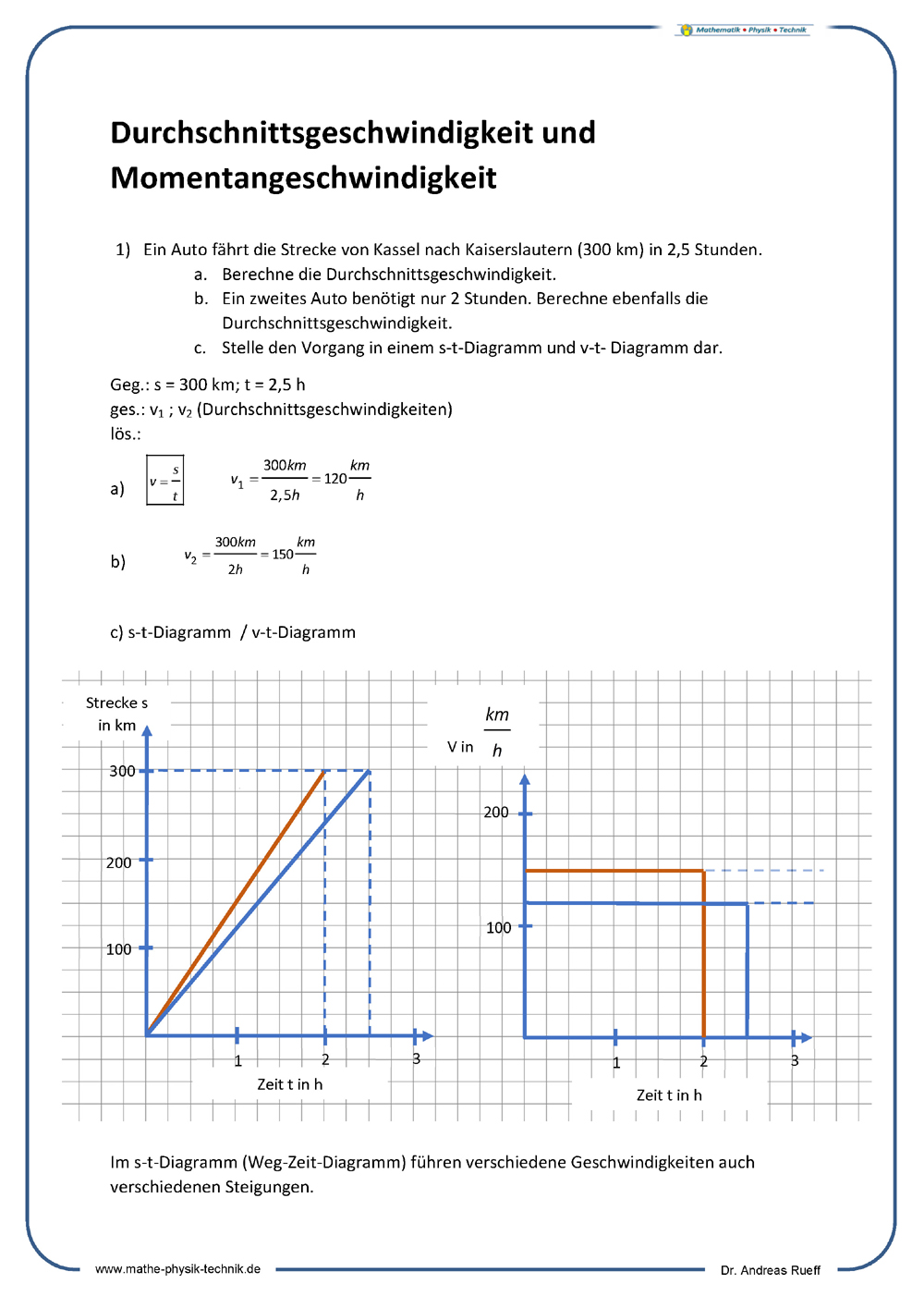
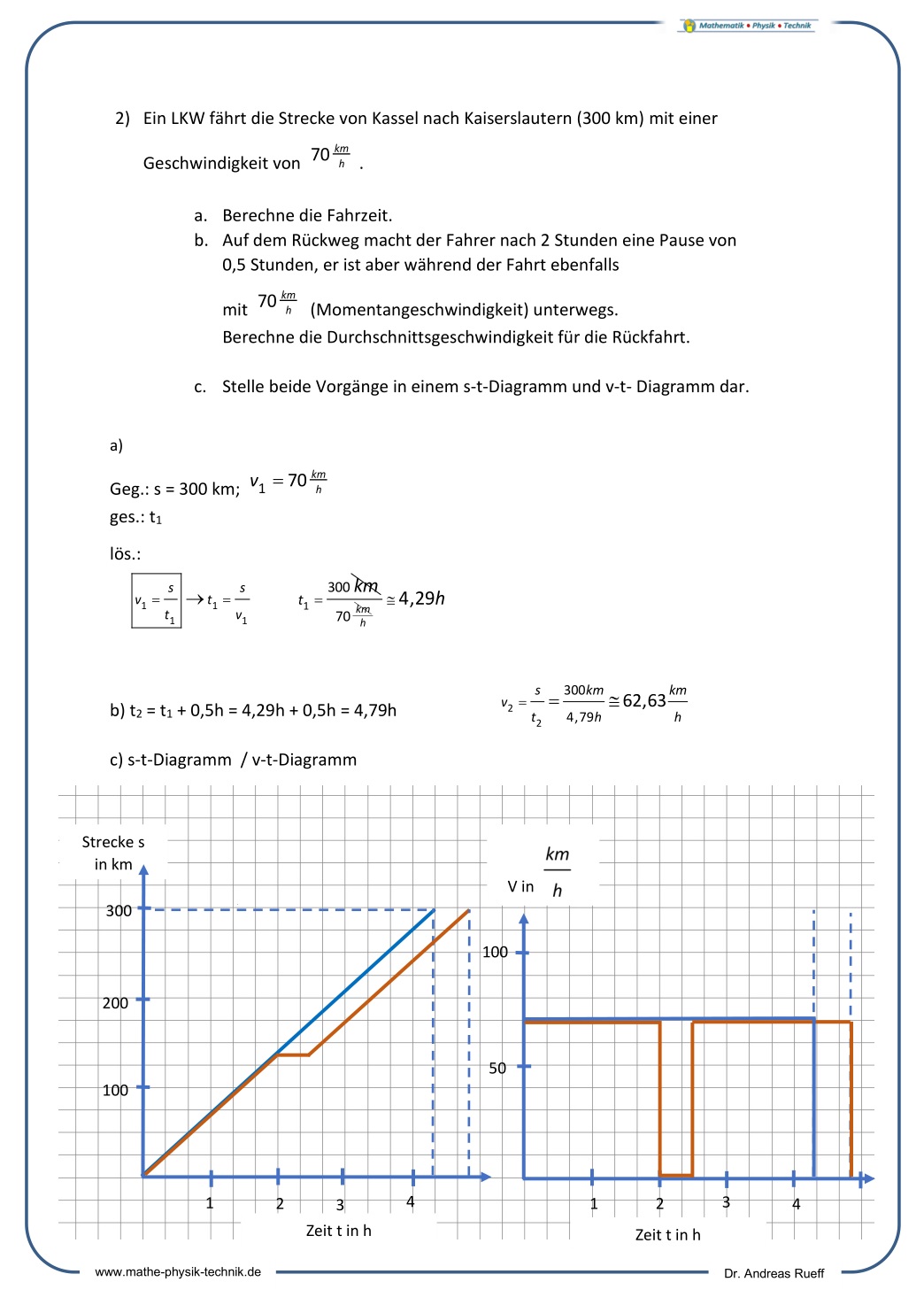
Aufgaben:
Durchschnittsgeschwindigkeit und Momentangeschwindigkeit
- Ein Auto fährt die Strecke von Fulda nach Kaiserslautern (220 km) in 1,9 Stunden.
- Berechne die Durchschnittsgeschwindigkeit.
- Stelle den Vorgang in einem s-t-Diagramm und v-t-Diagramm dar.
- Ein LKW fährt die Strecke von Kassel nach Köln (240 km) in 3,2 Stunden.
- Berechne die Durchschnittsgeschwindigkeit.
- Stelle den Vorgang in einem s-t-Diagramm und v-t-Diagramm dar.
- Auf der Rückfahrt ist der Fahrer mit der gleichen Geschwindigkeit (Momentangeschwindigkeit) auf der Autobahn unterwegs. Er macht aber nach zwei Stunden eine Pause von einer halben Stunde. Berechne die Durchschnittsgeschwindigkeit für die Rückfahrt.
- Erstelle für die Rückfahrt ein s-t-Diagramm und v-t-Diagramm.
- Ein Auto fährt die Strecke (570 km) von Kaiserslautern nach Dresden in 5,5 Stunden.
- Berechne die Geschwindigkeit für den Fall, dass der Fahrer ohne Pause die gesamte Strecke zurücklegt.
- Auf dem Rückweg legt der Fahrer nach 2 Stunden eine Pause von 30 Minuten ein, er benötigt dadurch für den Rückweg also länger. Berechne die Durchschnittsgeschwindigkeit für den gesamten Rückweg.
- Stelle beide Vorgänge in einem s-t-Diagramm und v-t-Diagramm dar.
- Von Berlin nach Leipzig legt ein Fahrer eine Strecke von 500 km zurück.
- Den Hinweg fährt der ohne Pause mit einer Durchschnittsgeschwindigkeit von . Wie lange benötigt er für die Strecke?
- Auf dem Rückweg legt er nach drei Stunden eine Pause von einer halben Stunde ein und benötigt für den Rückweg dadurch eine halbe Stunde länger. Berechne seine Durchschnittsgeschwindigkeit für den Rückweg.
- Stelle beide Fahrten in einem s-t-Diagramm und v-t-Diagramm dar.
- Von Köln nach Stuttgart beträgt die Strecke 370 km. Ein LKW fährt durchschnittlich mit 70 Kilometern pro Stunde.
- Wie lange ist der Fahrer unterwegs?
- Der Fahrer legt auf der Rückfahrt aber nach 3 Stunden eine Pause von 30 Minuten ein, fährt aber auch hier mit der Geschwindigkeit von 70 Kilometern pro Stunde. Wie lange ist er dann unterwegs? Berechne dafür seine Durchschnitts-geschwindigkeit.
- Stelle beide Vorgänge in einem s-t-Diagramm und v-t-Diagramm dar.
- Für die Strecke von Dresden nach Stuttgart benötigt ein LKW 7 Stunden. Die Strecke
beträgt 510 km. Der Fahrer hat dabei nach 4 Stunden eine Pause von 0,5 Stunden eingelegt.- Berechne seine Durchschnittsgeschwindigkeit für die gesamte Fahrt.
- Mit welcher Geschwindigkeit war der Fahrer während der Fahrzeit auf der Autobahn tatsächlich unterwegs (Momentangeschwindigkeit)?
- Stelle den Vorgang in einem s-t-Diagramm und v-t-Diagramm dar.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.

Physik - Mechanik: [8:23]
Gleichmäßig beschleunigte Bewegung (1)
Im Video wird von grundlegenden Überlegungen auf der Basis der gleichförmigen Bewegung der Wert der Erdbeschleunigung (g=9,81m/s²) abgeleitet. Dabei werden experimentell bestimmte Werten des freien Falls zugrunde gelegt.
Infotext - Die gleichmäßig beschleunigte Bewegung
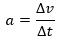
- Ein Fahrzeug bewegt sich zum Zeitpunkt t1=0s mit einer Geschwindigkeit von v1=10 m/s über die Straße. Fünfzehn Sekunden später, zum
Zeitpunkt t2=15s, beträgt die Geschwindigkeit v2=55 m/s. Die durchschnittliche Beschleunigung des Autos in diesem Zeitintervall war dann:
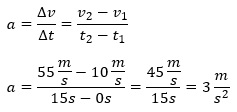
- Ein PKW, der vor der roten Ampel innerhalb von ∆t=3s von „Tempo 50“ (v1=50 km/h≈13,88 m/s) auf Null abgebremst wird, erfährt die
Beschleunigung:
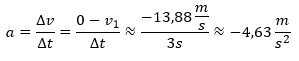
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Gleichmäßig beschleunigte Bewegung (1)
(freier Fall)
- Ein Stein fällt vom Humbergturm in Kaiserslautern. Der Turm hat eine Höhe von 35,8 Metern. Der Stein fällt 2,7 Sekunden bis er auf dem Boden auftrifft.
- Mit welcher Geschwindigkeit kommt der Stein unten an?
- Welche Durchschnittsgeschwindigkeit hat der der Stein? (Angabe in Kilometern pro Stunde)
- Ein Stein fällt vom Maintower in Frankfurt. Er legt dabei eine Strecke von 200 Metern zurück. Für den Fall benötigt der Stein 6,4 Sekunden.
- Mit welcher Geschwindigkeit kommt der Stein unten an?
- Welche Durchschnittsgeschwindigkeit hat der der Stein? (Angabe in Kilometern pro Stunde)
Zusatzfrage:
Vergleiche die Ergebnisse der ersten beiden Aufgaben. Was fällt dir auf?

Abb. 1: Humbergturm
Abb. 2: Maintower
- Das Empire State Building in New York hat eine Höhe von 381 Metern. Ein herunterfallender Stein benötigt 8,8 Sekunden bis er unten ankommt.
- Mit welcher Geschwindigkeit kommt der Stein unten an?
- Welche Durchschnittsgeschwindigkeit hat der der Stein? (Angabe in Kilometern pro Stunde)
- Vom Funkturm in Berlin fällt ein Stein herab. Bearbeite die folgenden Aufgaben der Reihe nach:
- Schau dir die Aufgaben 1-3 an. Notiere den allgemeinen Zusammenhang zwischen der Momentangeschwindigkeit beim Aufprall (v2) und der Durchschnittsgeschwindigkeit (vD) beim freien Fall.
- Berechne die Momentangeschwindigkeit beim Aufprall (v2), wenn die Durchschnittsgeschwindigkeit (vD) 26,8 Meter pro Sekunde beträgt.
- Wie lange dauert der freie Fall des Steins? Berechne mit dem Ergebnis aus Aufgabenteil c.
- Wie hoch ist der Funkturm?
--------------------------
Quellenangaben zu den Bildern:
Abb. 1 (Humbergturm): This file is licensed under the Creative Commons Attribution 2.5 Generic license. Author: Benjamin
Reinhard (https://commons.wikimedia.org/wiki/File:Humbergturm-Aussenansicht.jpg)
Abb. 2 (Maintower): This file is licensed under the Creative Commons Attribution (CC BY-SA 3.0 DE) license. Urheber: ©
Thomas Wolf, www.foto-tw.de (https://de.wikipedia.org/wiki/Datei:Maintower_Frankfurt.jpg)

Physik - Mechanik: [9:58]
Gleichmäßig beschleunigte Bewegung (2)
Im Video wird aus den grundlegenden Überlegungen des ersten Teils das Geschwindigkeits-Zeit-Gesetz und das Weg-Zeit-Gesetz eingeführt und abgeleitet. Einfache Anwendungsbeispiel werden vorgerechnet.
Videos:
1) → Was ist Beschleunigung | alpha Lernen erklärt Physik
2) → Geschwindigkeitsänderungen messen | alpha Lernen erklärt Physik
3) → Die Formel für Beschleunigung und ihre Umstellung | alpha Lernen erklärt Physik
4) → Diagramme für Beschleunigung und Geschwindigkeit | alpha Lernen erklärt Physik
5) → Bewegungsgesetze | alpha Lernen erklärt Physik
6) → Negative Beschleunigung | alpha Lernen erklärt Physik
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App ist wurde erstellt von A. Rueff nach einer Vorlage von woba55 bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App ist wurde erstellt von A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.

Infotext - Newton´sches Kraftgesetz
Das Newton´sche Kraftgesetz ist die Grundlage für eine genaue Beschreibung der Bewegung von Körpern. Seine Aussage lässt sich folgendermaßen in Worte fassen:
„Die Änderung der Bewegung ist der Einwirkung der bewegenden Kraft proportional und geschieht nach der Richtung derjenigen geraden Linie, nach welcher jene Kraft wirkt.“
Mit der „Änderung der Bewegung“ ist dabei die Änderung der Geschwindigkeit pro Zeitintervall gemeint. Formal wird dieser Zusammenhang zwischen Kraft und Bewegungsänderung ausgedrückt als:
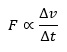
Das Zeichen zwischen der linken und der rechten Seite in diesem Zusammenhang bedeutet „proportional“, also „in festem Verhältnis stehend“. Die Aussage dahinter lautet: Die Änderung der Geschwindigkeit ∆v pro Zeitintervall ∆t ist proportional zur einwirkenden Kraft F. Der Ausdruck auf der rechten Seite ist uns aber bereits als „Beschleunigung“ bekannt, es gilt bekanntlich:
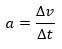
Entsprechend können wir diese Gleichung oben einsetzen, daraus folgt:
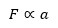
Das bedeutet, dass die einwirkende Kraft proportional zur Beschleunigung (also zur zeitlichen Änderung der Geschwindigkeit) eines Körpers ist.
Im Originalwerk von Newton wurde, in modernen Begriffen ausgedrückt, bereits eine allgemein gültige Formulierung verwendet, welche die Proportionalität von Kraft und Beschleunigung mit der
Masse m des betrachteten Körpers verbindet.
Es gilt: F = m ∙ a
In Worten ausgedrückt bedeutet das, dass die zeitliche Änderung der Geschwindigkeit eines Körpers der äußeren Kraft entspricht, die auf diesen Körper wirkt. Die Kraft kann
folglich als Ursache für die Beschleunigung des Körpers gesehen werden. (Dabei wird zudem auch die Möglichkeit einer Bewegungen von Körpern mit veränderlicher Masse -
beispielsweise Raketen – berücksichtigt).
Der Betrag der Geschwindigkeit ändert sich dabei unter der Voraussetzung, dass die betrachteten Kräfte und die Bewegung des Körpers in die gleiche Richtung
wirken. (Die Bewegungsrichtung des Körpers wird dagegen durch Kräfte geändert die senkrecht zur aktuellen Bewegungsrichtung stehen.) Die Gleichung
F = m ∙ a heißt Grundgleichung der Mechanik.
Isaac Newton
Sir Isaac Newton (1642 – 1726) war ein englischer Physiker, Astronom und Mathematiker an der Universität Cambridge und Leiter der Royal Mint (Münzprägeanstalt des Vereinigten
Königreichs).
Aufgrund seiner Leistungen, vor allem auf den Gebieten der Physik und Mathematik, gilt Sir Isaac Newton als einer der bedeutendsten Wissenschaftler aller Zeiten. Die von ihm
verfasste „Philosophiae Naturalis Principia Mathematica“ wird als eines der wichtigsten wissenschaftlichen Werke eingestuft.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
1) → Newton´sches Kraftgesetz - 2. Newtonsches Grundgesetz
3) → F = m * a | Kraft = Masse * Beschleunigung | Physik - Mechanik - einfach erklärt | Lehrerschmidt
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!


Infotext - Impuls und Kraftstoß
Impuls
Der Impulsbegriff entwickelte sich aus der Suche nach dem Maß für die in einem physikalischen Objekt vorhandene „Menge an Bewegung“. Daraus erklären sich die heute veralteten Bezeichnungen „Bewegungsgröße“ oder „Bewegungsmenge“ für den Impuls. Mit diesen Bezeichnungen konnte ursprünglich auch die Bewegungsenergie gemeint sein, das ist aber nicht das Gleiche! Erst Anfang des 19. Jahrhunderts wurden die Begriffe sauber unterschieden.
Der Impuls ist eine grundlegende physikalische Größe, die den mechanischen Bewegungszustand eines physikalischen Objekts charakterisiert. Der Impuls eines physikalischen Objekts ist umso größer, je schneller es sich bewegt und je massereicher es ist. Damit steht der Impuls für das, was in der Umgangssprache unscharf mit „Schwung“ und „Wucht“ bezeichnet wird. Das Formelzeichen des Impulses ist p (von lateinisch pellere ‚stoßen, treiben‘).
Die Einheit für den Impuls ist: (kg·m)/s [oder N·s]
Der Impuls hat einen Betrag und eine Richtung. Seine Richtung ist die Bewegungsrichtung des Objekts. Sein Betrag ist durch das Produkt aus der Masse des
Körpers und der Geschwindigkeit seines Massenmittelpunkts gegeben.
Der Impuls eines Körpers charakterisiert ausschließlich die geradlinige Bewegung seines Massenmittelpunkts. Eine eventuell zusätzlich vorhandene Rotation um den
Massenmittelpunkt wird dadurch nicht erfasst. Der Impuls ist eine additive Größe. Der Gesamtimpuls eines Objekts mit mehreren Bestandteilen ist die Summe der Impulse seiner Teile.
In der Formelsprache ausgedrückt lautet Definition für den Impuls:
p = m ∙ v
Der Impuls hängt, wie die Geschwindigkeit, von der Wahl des Bezugssystems ab. In einem geeigneten Bezugssystem ist der Impuls eine Erhaltungsgröße, das heißt: Ein Objekt, auf das von außen keine Kräfte wirken, behält seinen Gesamtimpuls nach Betrag und Richtung bei. Üben zwei Objekte Kraft aufeinander aus, z. B. bei einem Stoßvorgang, ändern sich ihre beiden Impulse in entgegengesetzter Weise so, dass ihre Summe (unter Beachtung der jeweiligen Richtung) erhalten bleibt. Die Größe, um die sich der Impuls für eines der Objekte ändert, wird als Impulsübertrag bezeichnet.
Kraftstoß
Um die Geschwindigkeit eines Körpers (nach Richtung und/oder Betrag) zu ändern, muss sein Impuls geändert werden. Die Impulsänderung p berechnet sich aus der dafür benötigten
Zeit t und der notwendigen Kraft F: p = F ∙ t
Diese Impulsänderung wird als Kraftstoß bezeichnet. Dabei spielen sowohl der Betrag als auch die Richtung der Kraft eine Rolle.
Die Einheit für den Kraftstoß ist: N·s
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
1) → Versuche zum elastischen und inelastischen Stoß
2) → Impuls einfach erklärt│Physik Lernvideo│Learning Level Up
3) → Impuls und Impulserhaltung – einfach erklärt
4) → Elastischer Stoß vs. Inelastischer Stoß
5) → Impuls & Impulserhaltung || Physik Tutorial
6) → Zentraler elastischer Stoß - einfache Fälle mit Formel und Erklärung
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
Aufgaben
-
Aus einer Pistole wir eine Kugel abgeschossen. Sie hat einen Impuls von
p = 4,6 (kg⋅m)/s und eine Masse von 11g. Mit welcher Geschwindigkeit fliegt die Kugel? -
Für den Vorgang im Beispiel auf der Folie "Impuls (2)" gilt für den Gesamtimpuls der beiden Wägen:
pges = p1 + p2 = 0.
Weiterhin gilt für den Impuls p = m⋅v . Das führt zur Gleichung:m1⋅v1 + m2⋅v2 = 0
Stelle diese Gleichung nach allen darin vorkommenden Variablen um (m1 ; m2 ; v1 ; v2) -
Betrachte den Versuch "B" von Folie (2) zum Inpuls: Der erste Wagen hat jetzt aber eine Masse von 400 g und nach den Durchtrennen der Schnur eine Geschwindigkeit von 2,3 m/s. Der zweite Wagen fährt mit der Geschwindigkeit von
5,2 m/s in die entgegengesetzte Richtung.
a) Welche Masse hat der zweite Wagen?
b) Berechne die Impulse der beiden Wagen nachdem die Schnur durchgeschnitten wurde.
c) Die wirkende Federkraft auf die beiden Wagen beträgt bei dem VorgangF = 5,75 N [Es gilt: 1N = 1(kg⋅m)/s2]. Berechne die Zeit in der die Federkraft auf den linken Wagen wirkt.
-
Eine Gewehrkugel (m = 8g) verlässt das Gewehr mit einer Geschwindigkeit von
350 m/s . Die Masse des Gewehrs beträgt 7 kg.
a) Berechne den Impuls der Kugel nachdem sie abgefeuert wurde.
b) Mit welcher Geschwindigkeit bewegt sich dabei das Gewehr in die entgegengesetzte Richtung? -
Ein Eisenbahnwaggon (Waggon A) trifft mit der Geschwindigkeit von 2 m/s auf zwei miteinander gekoppelte Waggons (Waggon B und C, zunächst stillstehend). Die Masse der drei Waggons beträgt jeweils 45 t. Dabei koppelt Waggon A an die beiden anderen miteinander verbundenen Waggons B und C an und bleibt mit ihnen verbunden. Mit welcher Geschwindigkeit bewegen sich die drei miteinander gekoppelten Waggons nach diesem inelastischen Stoß?
-
Wir betrachten jetzt die Situation von Aufgabe 4 nochmal. Der aufprallende Waggon A hat hier aber eine Geschwindigkeit von 3 m/s. Jetzt koppelt der aufprallende Waggon A aber nicht an die beiden anderen (miteinander verbundenen) Waggons B und C an. Die beiden miteinander gekoppelten Waggons haben nach diesem elastischen Stoß eine Geschwindigkeit von 2 m/s.
a) Beschreibe die Bewegung aller drei Waggons.
b) Berechne die Geschwindigkeit von Waggon A nach dem Stoß.
Video als Zusammenfassung der wichtigsten Inhalte zur Mechanik:
→ Einführung in die Physik: Newtonsche Mechanik (Physikus Lernteil)

Hier einige Links die dich auch interessieren könnten:
Die Seite ist für alle jungen Leute gedacht, die sich über Berufe und Ausbildungswege in der Luft- und Raumfahrt informieren wollen. Dazu gibt es jede Menge Infos.
Planet Schule
Planet Schule bietet Schulfernsehsendungen zum Ansehen und Herunterladen so wie weitere Lernangebote für Lehrer, Schüler und natürlich alle Bildungsinteressierten.
Alle von mir erstellten Materialien stehen für Bildungszwecke frei zur Verfügung, dürfen allerdings nicht von jemand anderem kommerziell vertrieben werden.
Hinweis: Es werden keine Bücher oder sonstige, hier benannte Materialien im Unterricht verwendet oder benötigt.
Quellenangaben zu den Inhalten auf dieser Seite
Infotext ([27] Mechanik - Bezugssysteme, Massenpunkte)
 Dieser Text basiert auf dem Artikel Bezugssystem aus der freien Enzyklopädie
Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported
(Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und
auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf dem Artikel Bezugssystem aus der freien Enzyklopädie
Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported
(Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und
auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Infotext ([28] Mechanik - Die Geschwindigkeit)
 Dieser Text basiert auf dem Artikel Geschwindigkeit aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf dem Artikel Geschwindigkeit aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Infotext ([29] Mechanik - Die beschleunigte Bewegung)
 Dieser Text basiert auf dem Artikel Beschleunigung aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf dem Artikel Beschleunigung aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Infotext ([31] Mechanik - Newton´sches Kraftgesetz)
 Dieser Text basiert auf den Artikeln Newtonsche Gesetze und Isaac Newton aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der
Text wurde von Andreas Rueff überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist
eine Liste der Autoren verfügbar.
Dieser Text basiert auf den Artikeln Newtonsche Gesetze und Isaac Newton aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der
Text wurde von Andreas Rueff überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist
eine Liste der Autoren verfügbar.
Infotext ([32] Mechanik - Impuls und Kraftstoß)
 Dieser Text basiert auf dem Artikel Impuls aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und auf der
Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf dem Artikel Impuls aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und auf der
Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Using PhET Simulations in Teaching
-
Simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0 (https://phet.colorado.edu).
Hintergrundbild: car-racing-4460629.jpg (Bearbeitet von A. Rueff)
Bild von mibro auf Pixabay
































