Mechanik (2)
Hier findest du alle Inhalte zur Unterrichtseinheit.
Inhalt - Mechanik
Körper und ihre Eigenschaften
Körper und Stoffe
Unterscheide zwischen Körpern und Stoffen
Größen und Einheiten
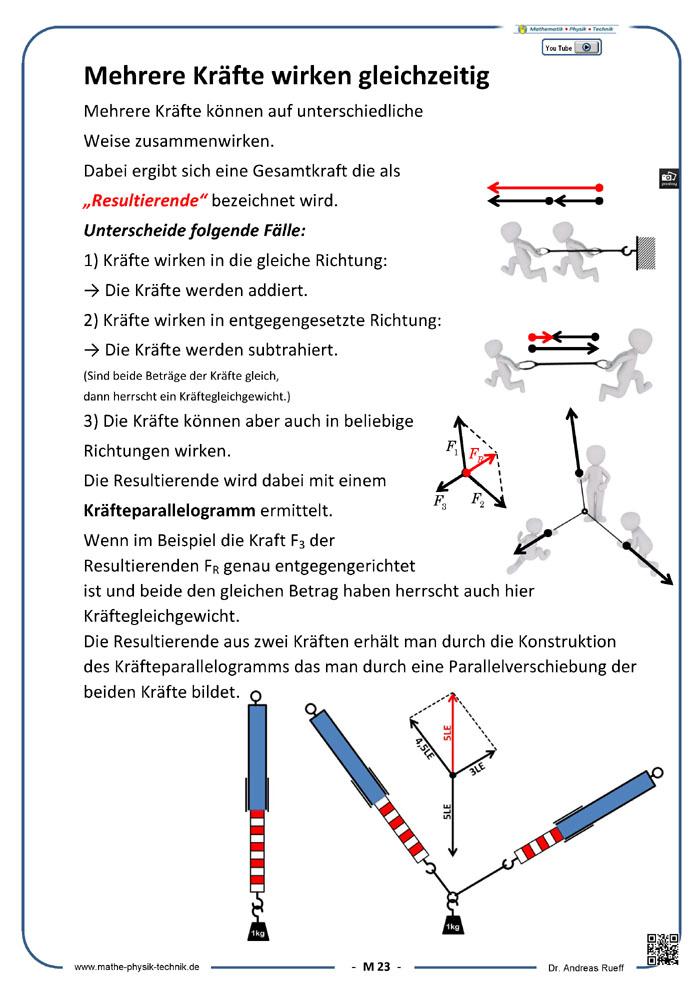
Kräfte und ihre Wirkung
Kräfte darstellen und messen
Kräfte werden gemessen – Aufgaben
Die Federkonstante
Schwere Masse / Träge Masse
Größenbereiche – Die Masse
Masseeinheiten
Die Grundeinheit ist das Kilogramm (1kg)
Das Volumen
Größenbereiche – Das Volumen
Die Dichte eines Körpers
Aufgaben zur Dichte
Der Auftrieb im Wasser
Schwimmen – schweben - sinken
Der Flaschentaucher
Teil 2:
Mehrere Kräfte wirken gleichzeitig
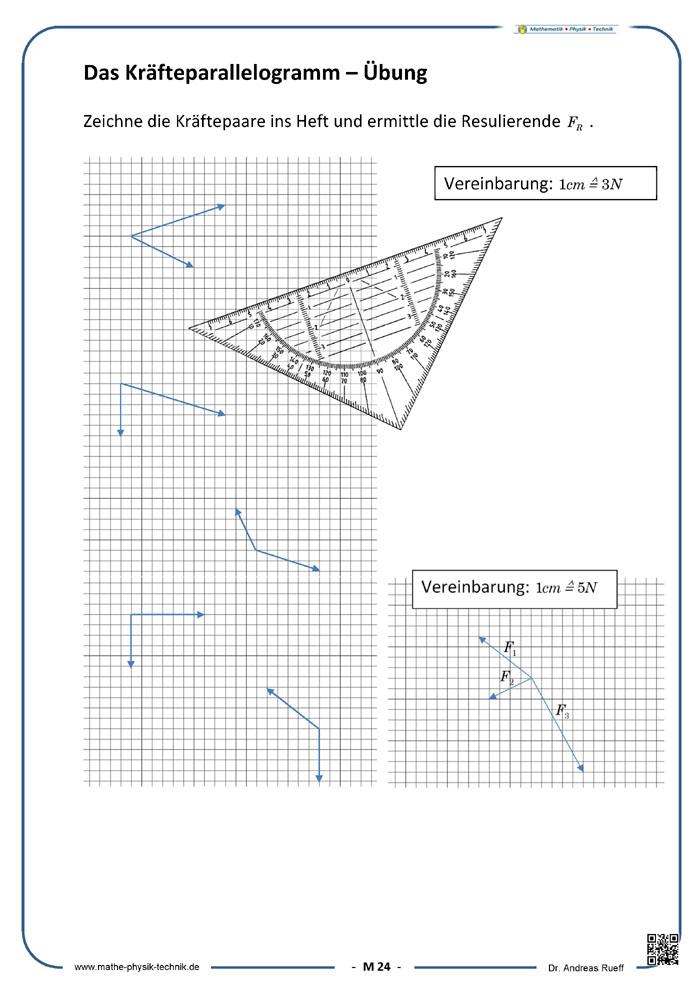
Das Kräfteparallelogramm – Übung
Flächenbelastung und Druck
Der Druck in Flüssigkeiten
Reibung
Drehmoment und Hebel
Kräfte umleiten – Seil, Stange, Rollen
Die Arbeit
Die Energie
Die mechanische Leistung
→ Teil 3 (Kinematik):
Die Bewegung von Körpern
Vorüberlegungen
Die Geschwindigkeit
Die beschleunigte Bewegung
Übersicht
Newton'sches Kraftgesetz
Impuls und Kraftstoß
Allgemeine Hinweise zu den Themenseiten
Die hier angebotenen Themenseiten fassen die grundlegenden Inhalte, Informationen und Hefteinträge zu den Unterrichtsinhalten von verschiedenen Themenbereichen der Fächer Mathematik, Physik und dem Wahlpflichtfach MINT/Technik zusammen. Diese sind online, kostenlos und ohne Registrierung verfügbar und sollen zur besseren Selbstorganisation der Schüler beitragen.
Die im Internet bereitgestellten Materialien bieten aber auch noch zusätzliche Möglichkeiten: Sie sollen den Schülern einen Leitfaden zur Vorbereitung auf Kursarbeiten, aber auch bei Fehlstunden zur Nacharbeit der versäumten Unterrichtsinhalte dienen und weiterhin den Eltern die Möglichkeit zur Unterstützung bei den unterrichtsbegleitenden Hilfestellungen geben. Die Zusammenfassungen zu den Unterrichtsinhalten auf den Themenseiten werden dabei jeweils ergänzt durch Lernvideos, Infotexten, Aufgaben, Bildergalerien und interaktiven Tools. Diese sollen dabei helfen selbstständig eigene Ergebnisse zu überprüfen oder zusätzliche Informationen zu den Inhalten erhalten. Bei den Lernvideos handelt es sich teilweise um die YouTube-Video des YT-Kanals Mathe-Physik-Technik. Weiterhin sind bei den einzelnen Folien zusätzliche Videovorschläge von anderen YouTube-Kanälen zugeordnet. Der jeweilige Link leitet dann ggf. direkt auf die YouTube-Video-Seite weiter.
Bei den klassischen physikalischen Themenbereichen sind die jeweiligen Folien für den digitalen Unterricht weitestgehend angepasst und optimiert worden. Insbesondere durch die Corona-Krise rückt der digitale und eigenverantwortliche Unterricht immer mehr in den Fokus. Zu den einzelnen Folien sind deshalb jeweils passende Videos zu den Inhalten zugeordnet und zu vielen Folien auch passende Aufgaben eingearbeitet worden. Dadurch sind die Themenbereiche in Teilabschnitten strukturiert und für die Arbeit mit Wochenplänen optimiert worden. Sie ermöglichen den Schülern so die selbstständige Arbeit daheim und geben jedem Schüler die Möglichkeit die Lernziele auch unter den gegebenen Umständen bestmöglich zu erreichen. Dabei können Schüler dann sogar die positiven Seiten des digitalen Unterrichts (Eigenes Lerntempo festlegen, optimale Anpassung von Lernzeit und Zeitpunkt an den eigenen Biorhythmus zum effizienten Lernen, etc.) für sich besonders gut nutzen.
Siehe hierzu auch: → Konzept - mathe-physik-technik.de
Skript → Publikationen
Bildergalerie 1
(Abbildungen mit freundlicher Genehmigung des DEUTSCHEN MUSEUMS München)
Flächenbelastung und Druck in Flüssigkeiten
In der Physik ist der Druck das Ergebnis einer senkrecht auf eine Fläche A einwirkenden Kraft F. Der mechanische Druck auf einer ebenen Fläche lässt sich mathematisch als Quotient schreiben:
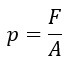
Das übliche Formelzeichen p lehnt sich an das lateinische bzw. englische Wort für Druck (lateinisch pressio, englisch pressure) an. Der Druck auf einen Körper ist
positiv, wenn die Kraft zu ihm hin gerichtet ist, ein negativer Druck entspricht einem Zug.
Blaise Pascal (1623-1662, französischer Mathematiker, Physiker, Literat und christlicher Philosoph) zu Ehren wird für den Druck die Einheit Pascal (mit dem
Einheitenzeichen Pa) verwendet, die einer Kraft von einem Newton (also der Gewichtskraft von etwa 100 Gramm) senkrecht verteilt auf einer Fläche von einem
Quadratmeter entspricht:
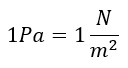
Flüssigkeiten und Gase
Druck in Flüssigkeiten und Gasen (Fluiden) breitet sich allseitig aus und wirkt im Volumen in alle Richtungen aber immer senkrecht auf Wände. Das wird als das Pascal‘sche
Prinzip bezeichnet, benannt nach dem französischen Physiker Blaise Pascal. Bei ruhenden Fluiden spricht man auch von hydrostatischem Druck.
Eine weitere gebräuchliche Einheit ist das Bar: 1 bar = 100000 Pa = 1000 hPa = 100 kPa
Druckmessgeräte
Absolutdruckmessinstrumente verwenden ein Vakuum als Bezugsdruck (z. B. Barometer).
Ein Druckmessgerät zum Anzeigen des physikalischen Druckes eines Mediums (Flüssigkeit, Gas) wird auch Manometer (– von altgriechisch manós „dünn“ und métron „Maß“) genannt.
In den meisten Anwendungen wird der Relativdruck – also bezogen auf den atmosphärischen Luftdruck – gemessen. Differenzdruckmessgeräte messen einen Druckunterschied zwischen zwei beliebigen
Systemen.

-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
1) → Druck berechnen - Physik | Lehrerschmidt - einfach erklärt!
3) → Schweredruck in Flüssigkeiten - Realexperiment
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
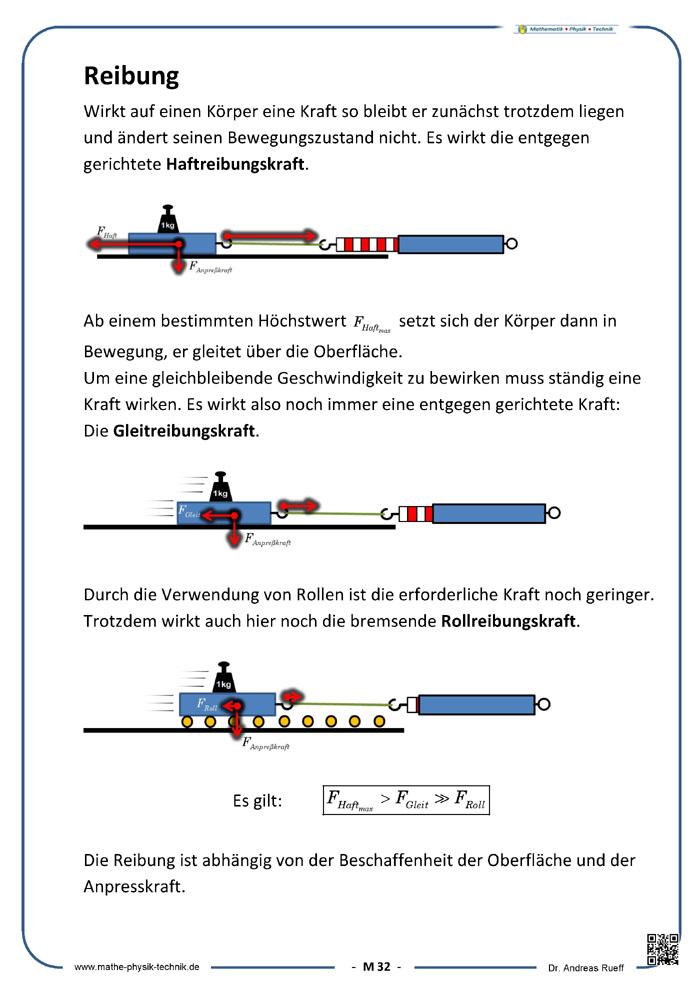
Reibung
Die Reibung, auch Reibungswiderstand genannt, ist eine Kraft, die zwischen Körpern oder Teilchen wirkt, die einander berühren. Die Reibungskraft erschwert dann die Bewegung der Körper gegeneinander. Um eine Bewegung zu erzeugen oder aufrechtzuerhalten, ist Energie notwendig. Wenn bei einer Bewegung Reibung auftritt, wird ein Teil der der Bewegungsenergie in Reibungswärme umgewandelt und/oder für Verschleiß verbraucht.
Bei der Betrachtung von Reibungsvorgängen unterscheidet man zwischen äußerer Reibung und innerer Reibung. Die äußere Reibung tritt auf bei Reibung zwischen sich berührenden Außenflächen von Festkörpern. Die innere Reibung tritt auf zwischen benachbarten Teilchen bei Verformungsvorgängen innerhalb von Festkörpern, Flüssigkeiten und Gasen.
Äußere Reibung
Äußere Reibung wird auch als Festkörperreibung bezeichnet, weil sie zwischen den Kontaktflächen von sich berührenden Festkörpern auftritt. Wir unterscheiden Haftreibung, Gleitreibung und Rollreibung.
→ Haftreibung
In vielen Fällen ist Haften zwischen sich berührenden Körpern erwünscht. Ohne Haftreibung würde der Alltag gar nicht funktionieren. Möbel würden nicht an ihrem Platz bleiben, auf der Straße abgestellte Fahrzeuge (die Räder blockiert) könnten allein vom Wind fortbewegt werden. Man könnte keinen Fuß „fest“ auf den Boden setzen, alle angetriebenen Fahrzeugräder würden „durchdrehen“. In technischen Anwendungen wird deshalb außer der meistens wirkenden Gewichtskraft oft auch ein technisch erzeugter Druck zwischen den Kontaktflächen erzeugt.
→ Gleitreibung
Gleitreibung tritt an den Kontaktflächen zwischen Körpern auf, die sich relativ zueinander bewegen. Die Gleitreibungskraft ist meist geringer als die Haftreibungskraft, sie ist unabhängig von der Geschwindigkeit.
→ Rollreibung
Rollreibung ist die Kraft, die beim Abrollen eines Rades entsteht und der Bewegung des Körpers entgegengerichtet ist. Bei vergleichbaren Rahmenbedingungen ist die Rollreibung erheblich kleiner als die Gleitreibung. Die Kraft, die überwunden werden muss, um einen runden Körper aus dem Stillstand in rotierende Bewegung zu versetzen, wird als Anfahrwiderstand bezeichnet.
Innere Reibung
Innere Reibung bewirkt die Zähigkeit von Materialien und Fluiden und hat Einfluss auf Verformungen und Strömungen. Neben der Bewegung der Teilchen in einem Stoff beschreibt die innere Reibung auch den Reibungswiderstand von Körpern, die sich in Fluiden bewegen. Typischerweise nimmt in Gasen die innere Reibung mit der Temperatur zu, und in Flüssigkeiten ab.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
1) → Reibung
2) → Reibung - Haftreibung, Gleitreibung, Rollreibung
3) → Reibung I Haftreibung und Gleitreibung I musstewissen Physik
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
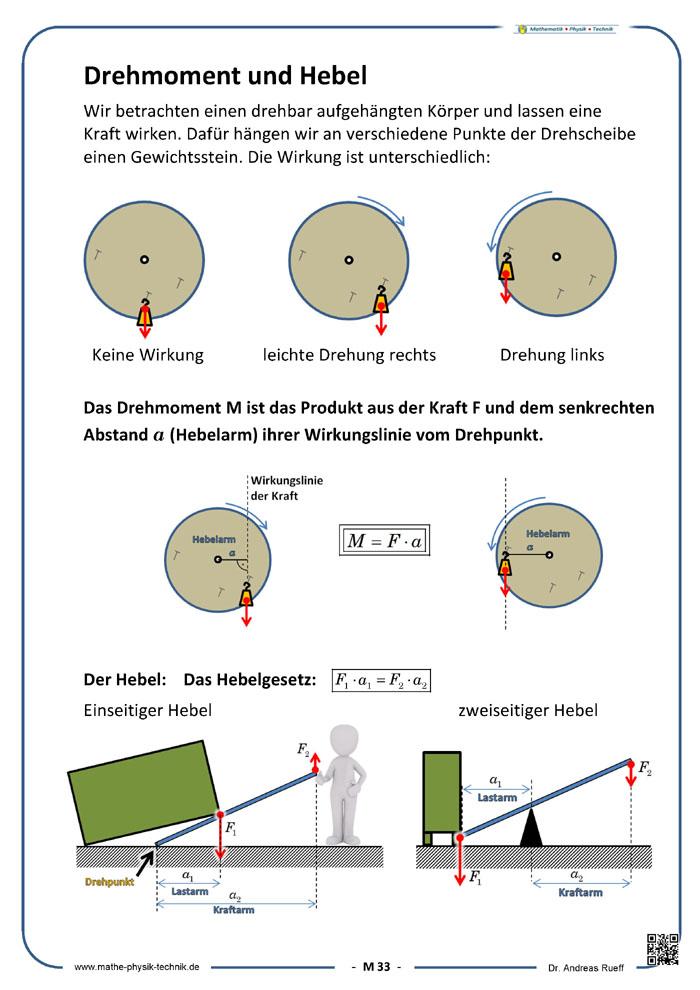
Drehmoment und Hebel
Ein Hebel ist ein wertvolles Werkzeug das uns beim Anheben einer schweren Last erlaubt Kraft „einzusparen“. Der Hebel ist ein mechanischer Kraftwandler bestehend aus einem
starren Körper (z.B. eine Stange), der um einen Drehpunkt drehbar ist.
Unterschieden werden einseitige und zweiseitige Hebel, je nachdem ob die Kräfte nur auf einer Seite oder auf beiden Seiten des Drehpunktes (siehe Folie) angreifen.
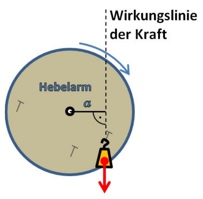
Die zentrale physikalische Größe, die zur Beschreibung eines Hebels benötigt wird, ist das Drehmoment M in Bezug auf den Drehpunkt, um den sich der Hebel drehen kann. Das Drehmoment (lat. momentum Bewegungskraft) ist eine physikalische Größe, die die Drehwirkung einer Kraft auf einen Körper bezeichnet. Ein Drehmoment kann die Rotation eines Körpers beschleunigen oder bremsen oder den Körper verbiegen. Der senkrechte Abstand zwischen der Wirkungs¬linie der Kraft und dem Bezugspunkt wird Hebelarm genannt. Das Drehmoment ist das Produkt aus wirkender Kraft und Hebelarm: M=F∙a
Beim Hebel wirken zwei Drehmomente, im Gleichgewicht sind beide Drehmomente gleich aber entgegengesetzt gerichtet. Die mathematische Beschreibung eines Hebels erfolgt durch
das Hebelgesetz: F1∙a1=F2∙a2
Mit einem großen Hebelarm kann mit einer kleinen Kraft ein großes Drehmoment ausgeübt werden. Dieser Umstand veranlasste Archimedes (287 – 212 v. Chr.; griechischer Mathematiker,
Physiker und Ingenieur) zu der Bemerkung:
„Gebt mir einen festen Punkt im All, und ich werde die Welt aus den Angeln heben.“
In der Technik werden Hebel durch ihre drei Komponenten beschrieben:
Lastarm a1: Hebelarm auf der Seite der zu bewegenden Last
Kraftarm a2: Hebelarm auf der Seite der bewegenden Kraft
Drehpunkt: Punkt, um den sich der Hebel drehen kann
Mit diesen Bezeichnungen lautet das Hebelgesetz:
„Kraft mal Kraftarm ist gleich Last mal Lastarm“
Anwendungen
Hebel finden sich in vielen technischen und alltäglichen Dingen wieder. Beim Rudern findet das Hebelgesetz Anwendung, indem die Sportler durch eine große Kraft am kurzen Ende einen weiten Weg am langen Ende des Ruders zurücklegen, was zu einer großen Geschwindigkeit führt. Auf Kinderspielplätzen finden sich Hebel in Form von Wippen. Dort wird die Wippe durch wechselseitiges Anlegen einer Kraft hin- und hergeschwenkt. Balkenwaagen nutzen das Hebelgesetz, um Gewichte zu vergleichen. Eine Zange verstärkt die Handkraft. Gleiches gilt bei einem Nussknacker. Schaufel und Brechstange können an der Front hohe Kräfte ausüben, weil die Armkraft an einem langen Stiel ansetzt.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
1) → Hebelgesetze I musstewissen Physik
2) → Drehmoment berechnen + Erklärung des Hebelgesetz - einfach erklärt mit Beispielen
3) → Hebelgesetz - einseitiger und zweiseitiger Hebel | Physik - einfach erklärt | Lehrerschmidt
4) → Hebelgesetze – Wie funktioniert ein Nussknacker?
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
Aufgaben: Drehmoment und Hebel
- Hebel helfen uns im Alltag in vielen verschiedenen Situationen. Abb. 1 zeigt dir einen Nussknacker. Beschreibe die Funktionsweise, skizziere ihn in deinem Heft und benenne den Lastarm,
den Kraftarm und den Drehpunkt.

- In Abb. 2 siehst du eine Wippe. Paul und Anja wollen wippen, Anja ist aber leichter als Paul. Beide stellen sich zunächst auf eine Wage, bei Anja werden 35 kg angezeigt, bei Paul sind es
45 kg. Wie müssten sich beide auf die Wippe setzen? Es gibt verschiedene Möglichkeiten. Mach einen Vorschlag und erläutere deine Überlegungen.

- In Abb. 3 siehst du die Tretkurbel und das Zahnrad eines Fahrrads. Auch hier nutzen wir die Funktion eines Hebels. Beschreibe die Funktion anhand einer Skizze. Benenne auch hier Lastarm,
Kraftarm und Drehpunkt.

- In den Abbildungen 4 und 5 siehst du ein Gerät das einer Wippe ähnelt. Es herrscht jeweils ein Gleichgewicht. Welche Kraft zeigt der Kraftmesser dabei in Abb. 4 und Abb. 5 an?
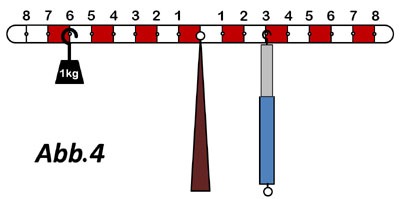
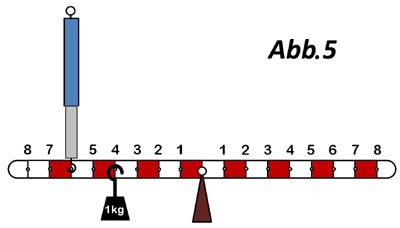
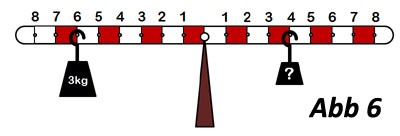
- Das Gerät aus Abb. 6 soll jetzt verwendet werden. Die Markierungen auf dem Gerät haben jeweils einen Abstand von 2 cm. Auf der linken Seite hängt eine Masse von 3kg an der Markierung mit
der Nummer 6, also 6cm vom Drehpunkt entfernt. Es soll ein Gleichgewicht hergestellt werden.
a) In der Abbildung ist an Position 4 auf der rechten Seite ein Wägestück angehängt. Welche Masse muss es zur Herstellung eines Gleichgewichts haben?
b) Welche Masse müsste auf der rechten Seite an der Markierung mit der Nummer 6 angehängt werden?
c) Welche Masse müsste auf der rechten Seite an der Markierung mit der Nummer 3 angehängt werden?
d) Welche Masse müsste auf der rechten Seite an der Markierung mit der Nummer 7 angehängt werden?
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
1) → Wie funktioniert ein Flaschenzug? I musstewissen Physik
2) → Flaschenzug mit mehreren Rollen I musstewissen Physik
3) → Umlenkrolle (feste Rolle) | Physik - Mechanik - einfach erklärt | Lehrerschmidt
4) → Lose Rolle | Physik - Mechanik - einfach erklärt | Lehrerschmidt
5) → Flaschenzug - Physik einfach erklärt! | Lehrerschmidt
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
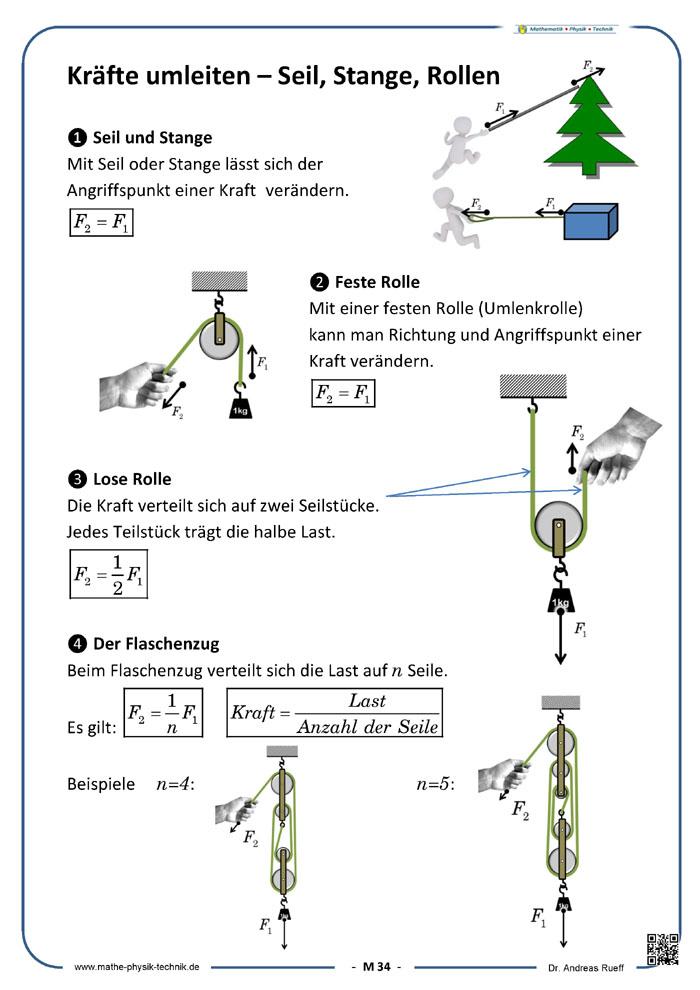
Aufgaben: [22] Kräfte umleiten
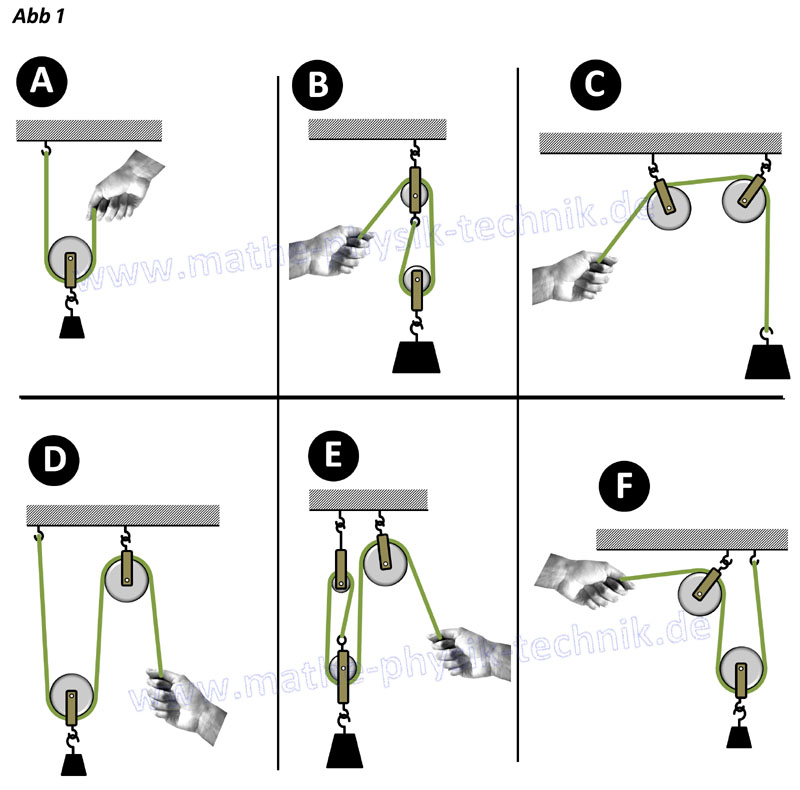
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise
(manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Die Arbeit
Beim Begriff „Arbeit“ ist es sehr wichtig zwischen der physikalischen und der umgangssprachlichen Bedeutung zu unterscheiden! Umgangssprachlich „wird gearbeitet“, um beispielsweise Geld zu verdienen. Die Formulierungen „man geht zur Arbeit“ oder „man hat noch viel Arbeit“ werden oft verwendet. Dabei wird aber nicht immer im physikalischen Sinn auch Arbeit verrichtet!
Eine anschauliche Bedeutung der physikalischen Größe ist die „Mühe“, die man beim Anheben eines schweren Gegenstandes hat. Zwar kann man sich diese Aufgabe scheinbar erleichtern, indem man einen Flaschenzug oder ein ähnliches Hilfsmittel verwendet. Dadurch wird die erforderliche Kraft tatsächlich geringer. Derlei Hilfsmittel werden daher auch Kraftwandler genannt. Dies erkauft man sich jedoch damit, dass man eine weitere Strecke zurücklegen muss. Beispielsweise ist der geneigte Weg auf einer schiefen Ebene (Rampe) länger als die senkrechte Höhendifferenz, um die der Gegenstand gehoben wird. Es zeigt sich, dass die Strecke im selben Maße zunimmt, wie sich die Kraft durch das Hilfsmittel verringert (→ Goldene Regel der Mechanik). Das Produkt aus beiden Größen „Kraft mal Weg“ ist also in allen Fällen gleich, wenn man von Reibung und ähnlichen Störeinflüssen absieht. Daher erscheint es sinnvoll, eine physikalische Größe zu definieren, die diesen Arbeitsaufwand unabhängig von der angewendeten Methode beziffert. Diese Größe erhält die Bezeichnung Arbeit mit der Berechnungsgleichung:
W = F∙s
Hierbei ist W (engl. work) die Arbeit, F die Kraft und s die zurückgelegte Strecke. Die Definition der rein mechanischen Arbeit lautet „Arbeit ist gleich Kraft mal Weg“.
Die physikalische Arbeit wird in der Einheit Joule (J) angegeben, benannt nach dem britischen Brauer und Physiker James Prescott Joule (1818 – 1889). Er war selbst Besitzer
einer Bierbrauerei und forschte, ausgehend von technischen Fragen des Maschinenbaus und des Brauereiwesens, zu naturwissenschaftlichen Fragen. Beispiel: Die physikalische Arbeit von 1J wird
verrichtet, um eine Masse von 100g (eine Tafel Schokolade) um einen Meter nach oben zu heben (vom Boden auf einen Tisch).*
Es gilt: 1J = 1Nm ( = 1 Ws)
(Anmerkung: Formal ähnelt die Einheit der Arbeit derjenigen des Drehmoments: „Newtonmeter“. Da aber die physikalischen Hintergründe völlig verschieden sind,
sollten die Einheiten nicht gleichgesetzt werden).
* Das gilt auf der Erde unter Berücksichtigung der Näherung g = 10 m/s2
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
2) → Arbeit (W=F*s) | Was ist das? | Physik - Mechanik - einfach erklärt | Lehrerschmidt
3) → Hubarbeit (W=F*h) Was ist das ? | Physik - Mechanik - einfach erklärt | Lehrerschmidt
4) → Mechanische Arbeit: Was ist das? – Physik | Duden Learnattack
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
Aufgaben - Mechanik - Die Arbeit
- Erkläre den Unterschied zwischen der umgangssprachlichen und der physikalischen Bedeutung des Begriffs „Arbeit“. Erläutere deine Überlegungen an jeweils zwei Beispielen.
- Wo wird hier (Abb. 1) im physikalischen Sinn Arbeit verrichtet? Beschreibe kurz das Bild und begründe deine Entscheidung.
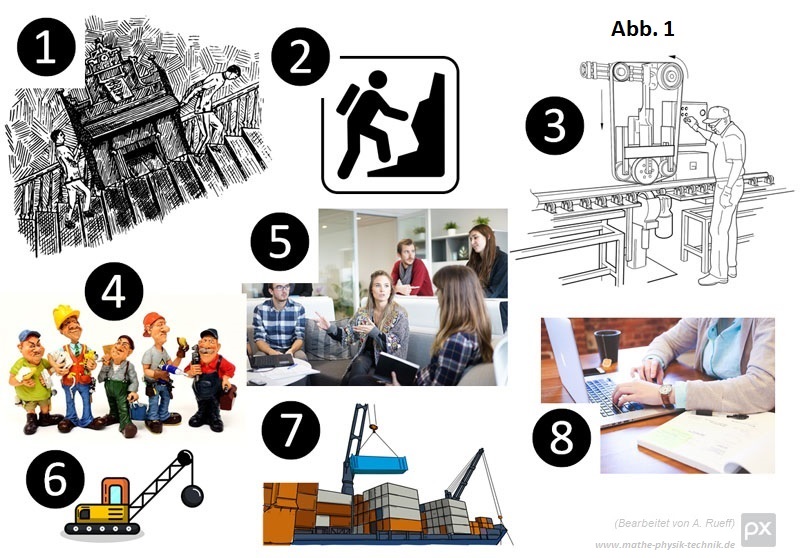
- Paul trägt einen Stein vom Erdgeschoss in das 4. Obergeschoss. Der Stein hat eine Masse von 15kg. Von einem Stockwerk zum nächsten Stockwerk überwindet er dabei jeweils 3 Meter. Welche Arbeit wurde dabei verrichtet?
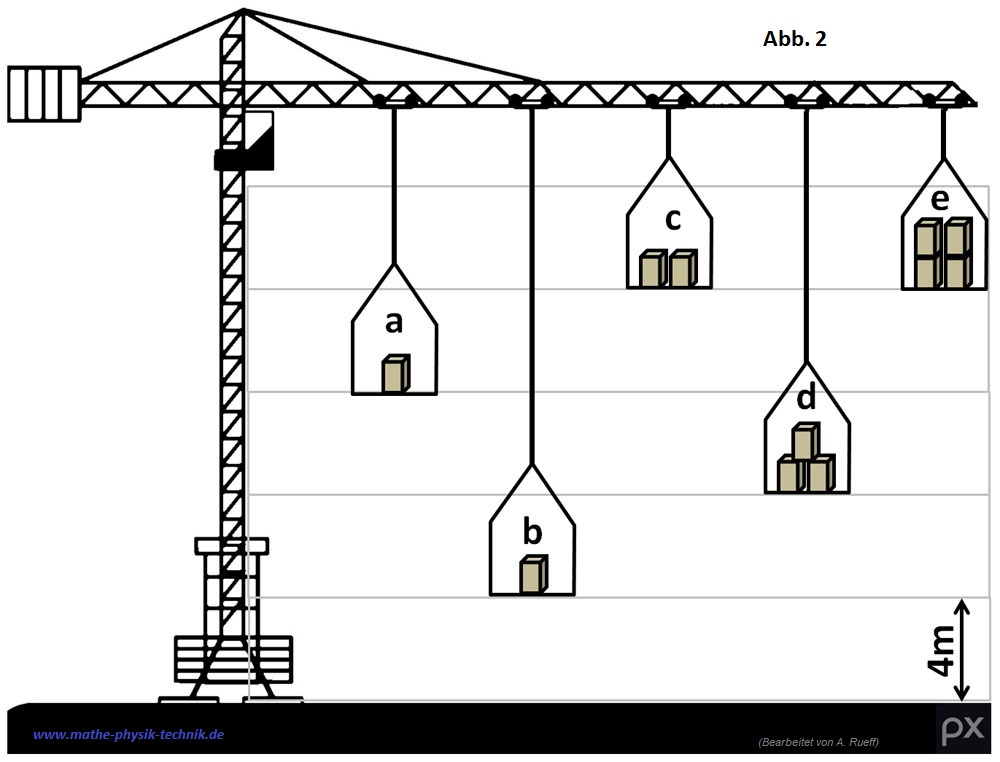
- Der Kran in Abb. 2 hebt Lasten hoch. Dabei verrichtet er Arbeit. Eine Kiste hat eine Masse von 250kg. Berechne die verrichtete Arbeit.
- Stelle die Formel zur Berechnung der physikalischen Arbeit nach allen darin vorkommenden Variablen um:
a) … nach F:
b) … nach s: - Ein Kran hat eine Masse von 850kg nach oben gezogen und dabei eine Arbeit von 153000Nm verrichtet. Um welche Höhe wurde die Masse angehoben?
- Drei Männer haben eine Waschmaschine ausgeliefert und sie dort in die Wohnung getragen. Diese ist im 5. Obergeschoss, Sie haben dabei eine Höhe von 15 Metern überwunden. Wir gehen davon aus, dass alle drei Männer den gleichen Anteil der Arbeit verrichten haben. Jeder der Männer hat eine Arbeit 4000J verrichtet. Welche Masse hat die Waschmaschine?
Goldene Regel der Mechanik
Bei Kraftwandlern (Hebel, Flaschenzug, schiefe Ebene) wird oft angestrebt, eine aufzubringende Kraft (z. B. die Gewichtskraft zum Anheben eines Gegenstandes) durch eine kleinere zu ersetzen. Man kann dabei zwar die nötige Kraft reduzieren, die zu verrichtende Arbeit bleibt aber gleich.
Galileo Galilei formulierte im Jahr 1594: „Was man an Kraft spart, muss man an Weg zusetzen“. Die Goldene Regel der Mechanik drückt den Inhalt des Energieerhaltungssatzes für einfache Beispiele der Mechanik aus.
Der Energieerhaltungssatz besagt, dass Energie weder erzeugt noch vernichtet werden kann. Energie kann aber zwischen verschiedenen Energieformen umgewandelt werden, beispielsweise von Bewegungsenergie in Wärmeenergie. Die Gesamtenergie eines abgeschlossenen Systems ändert sich mit der Zeit aber nicht.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
1) → Goldene Regel der Mechanik | Physik- einfach erklärt - Lehrerschmidt
2) → Goldene Regel der Mechanik (Galileo Galilei) | Mechanik | Physik | Lehrerschmidt
3) → Die goldene Regel der Mechanik – Physik | Duden Learnattack
4) → Flaschenzug - Physik einfach erklärt! | Lehrerschmidt
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
Die Energie
Die Energie (oder auch Energiemenge) ist eine fundamentale physikalische Größe, die in allen Teilgebieten der Physik sowie in der Technik, Chemie, Biologie und der Wirtschaft eine zentrale Rolle spielt. Die physikalischen Größen Energie und Arbeit hängen eng miteinander zusammen:
Energie ist gespeicherte Arbeit, sie beschreibt die Fähigkeit eines Systems, Arbeit zu verrichten.
Energie wird deshalb ebenfalls in der Einheit Joule (=Nm) angegeben. 1841 veröffentlichte der deutsche Arzt Julius Robert Mayer die Idee, dass Energie weder erschaffen noch vernichtet, sondern nur umgewandelt werden kann. In einem gegenüber der Umgebung abgeschlossenen System ändert sich die Gesamtenergie also demnach nicht. Das ist die Aussage des Energieerhaltungssatzes. Eine Dampfmaschine wandelt beispielsweise Wärmeenergie in mechanische Energie um. Die Wärmeenergie, die während des Betriebs einer Dampfmaschine verloren gegangen ist, entspräche genau der mechanischen Arbeit, die die Maschine leistet.
Energieformen
Energie gibt es in verschiedenen Energieformen, die ineinander umgewandelt werden können. von Energieformen sind Lageenergie (potentielle Energie), Bewegungsenergie (kinetische Energie), elektrische, chemische und Wärmeenergie (thermische Energie). Beispiele für solche Umwandlungen von Energie sind, dass ein Mensch ein Paket hochhebt (Beim Herunterfallen wird die potentielle Energie dann wieder frei) oder eine Batterie aufgeladen wird.
Technische Nutzung der Energie
Eine Erzeugung von Energie ist aufgrund des Energieerhaltungssatzes nicht möglich. Die Bezeichnung „Energieerzeugung“ wird im Wirtschaftsleben aber dennoch verwendet, um die
Umwandlung einer bestimmten Energieform (zum Beispiel elektrischer Strom) aus einer anderen Form (zum Beispiel chemischer Energie in Form von Kohle) auszudrücken. Analog gibt
es im strengen physikalischen Sinne auch keinen „Energieverbrauch“, wirtschaftlich gemeint ist damit der Übergang von einer Energieform in eine andere.
Beispielsweise wird elektrische Energie „verbraucht“, um einen Ventilator zu betreiben. Die „verbrauchte“ elektrische Energie muss dann von uns bezahlt werden. Von
Energieeinsparung ist die Rede, wenn effizientere Prozesse gefunden werden, die weniger Primärenergie (Kohle, Gas, Öl) für denselben Zweck benötigen, oder anderweitig, zum
Beispiel durch Konsumverzicht, der Primärenergieeinsatz reduziert wird.
Die meisten Umwandlungen erfolgen nicht vollständig in eine einzige Energieform, sondern es wird ein Teil der Energie in Wärme gewandelt. In mechanischen Anwendungen wird die
Wärme meist durch Reibung erzeugt. Diese Wärme wird in der Regel nicht genutzt und als „Verlust“ bezeichnet. Das Verhältnis zwischen erfolgreich umgewandelter Energie und
eingesetzter Energie wird Wirkungsgrad genannt. Bei technischen Anwendungen wird häufig eine Reihe von Energieumwandlungen gekoppelt. In einem Kohlekraftwerk wird zunächst
die chemische Energie der Kohle durch Verbrennung in Wärme umgesetzt und auf Wasserdampf übertragen. Turbinen wandeln die Wärme des Dampfs in mechanische Energie um und treiben wiederum
Generatoren an, die die mechanische Energie in elektrische Energie umwandeln.
Während alle Energieformen unter gewissen Bedingungen vollständig in thermische Energie umgewandelt werden können, gilt das in umgekehrter Richtung nicht. Abhängig von der
Temperatur, bei der die Wärme zur Verfügung steht, lässt sich nur ein mehr oder weniger großer Anteil in mechanische Arbeit umwandeln, während der Rest an die Umgebung abgegeben wird.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
1) → Welche Energieformen gibt es?
2) → Energieformen - Überblick REMAKE
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.

Infotext - Mechanische Leistung

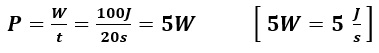
Wird dieselbe Energie in einer kürzeren Zeit bezogen, dann ist die Leistung größer; bei Bezug von W = 100 J in einer Zeitspanne von t = 10 Sekunden:
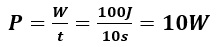
Leistungsangaben im Alltag
Im physikalisch-technischen Zusammenhang wird der Begriff Leistung in verschiedenen Bedeutungen verwendet. Die Hersteller elektrischer Geräte sind zur Angabe der maximalen
Leistungsaufnahme verpflichtet, also der Leistung, die der Energieversorgung (Stromnetz, Batterie) maximal entnommen wird (Kennzeichen eines Gerätes oder einer Anlage; auch
Nennleistung genannt). Die tatsächlich abgegebene Leistung kann weit geringer sein je nach Wirkungsgrad, d. h. nach Abzug der Energieverluste bei der Wandlung der elektrischen Energie in
die gewünschte Energieart. Wärmeverluste, mechanische und andere Verluste reduzieren die tatsächliche abgegebene Leistung z.B. einer Bohrmaschine oder eines Staubsaugers.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Infotext - James Watt
James Watt (1736 - 1819) war ein schottischer Erfinder. Seine einflussreichste Erfindung war die Verbesserung des Wirkungsgrades der Dampfmaschine.
 Watt wurde als Sohn armer, gebildeter Eltern geboren. Sein Vater war Zimmermann und
Konstrukteur von nautischen Geräten. Schon als Junge experimentierte er gern und soll die Funktionsweise von jedem Gegenstand, den er in die Finger bekam, erforscht haben. Für ein
Medizinstudium, für welches Watt sich interessierte, waren seine Eltern jedoch zu arm. Deshalb begann Watt in London eine inoffizielle Mechanikerlehre. Watt erhielt
1757 eine Stelle als Instrumentenmacher an der Universität von Glasgow. Sein Einraum-Labor entwickelte sich schon bald zum Treffpunkt von Dozenten und Studenten. Watt fand an der Universität
viele Freunde, obwohl er „nur“ ein Handwerker war.
Watt wurde als Sohn armer, gebildeter Eltern geboren. Sein Vater war Zimmermann und
Konstrukteur von nautischen Geräten. Schon als Junge experimentierte er gern und soll die Funktionsweise von jedem Gegenstand, den er in die Finger bekam, erforscht haben. Für ein
Medizinstudium, für welches Watt sich interessierte, waren seine Eltern jedoch zu arm. Deshalb begann Watt in London eine inoffizielle Mechanikerlehre. Watt erhielt
1757 eine Stelle als Instrumentenmacher an der Universität von Glasgow. Sein Einraum-Labor entwickelte sich schon bald zum Treffpunkt von Dozenten und Studenten. Watt fand an der Universität
viele Freunde, obwohl er „nur“ ein Handwerker war.
Weiterentwicklung der Dampfmaschine
1764 erhielt Watt als Universitätsmechaniker den Auftrag, das Modell einer Dampfmaschine zu reparieren. Watt beschloss, die Maschine zu verbessern. Watt gab seine Stelle an der Universität Glasgow auf, um sich stärker der Weiterentwicklung der Dampfmaschine zu widmen. Erst 1769 fand er dann aber die notwendigen Geldgeber und reichte 1769 das englische Patent ein. Watts Verbesserungen ermöglichten eine Ersparnis an Steinkohle von über 60 Prozent. Die erste einsatzfähige Dampfmaschine nach dem Wattschen Prinzip wurde 1776 installiert. Durch Watts Ideen wurden wesentlich stärkere Maschinen möglich. Auch führte er die Pferdestärke (PS) als Maßeinheit für die Leistung ein (1PS = 0,74kW; 1 kW = 1,36PS). .
Wettbewerber
Watt und sein Geldgeber Matthew Boulton behinderten während der Zeit, in der die Watt verliehenen Patente Gültigkeit hatten, erfolgreich die Weiterentwicklung der Dampfmaschine durch konkurrierende Ingenieure.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
1) → Leistung (P=W/t) Was ist das? | Physik - Mechanik - einfach erklärt | Lehrerschmidt
2) → Mechanische Leistung und Arbeit I musstewissen Physik
3) → Mechanische Leistung & Arbeit
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
Siehe auch → Themenseite: Elektrizität
Siehe auch → Themenseite: Technische Industrialisierung

Hier einige Links die dich auch interessieren könnten:
Das TECHNOSEUM ist eines der großen Technikmuseen in Deutschland. Die Ausstellung zeigt 200 Jahre Technik- und Sozialgeschichte. Sie steht mit ihren Experimentierstationen zu Naturwissenschaft und Technik für experimentelles Begreifen mit Spaß und Staunen. Kommen Sie mit auf eine interaktive Zeitreise!
Planet Schule
Planet Schule bietet Schulfernsehsendungen zum Ansehen und Herunterladen so wie weitere Lernangebote für Lehrer, Schüler und natürlich alle Bildungsinteressierten.
Alle von mir erstellten Materialien stehen für Bildungszwecke frei zur Verfügung, dürfen allerdings nicht von jemand anderem kommerziell vertrieben werden.
Hinweis: Es werden keine Bücher oder sonstige, hier benannte Materialien im Unterricht verwendet oder benötigt.
Quellenangaben zu den Inhalten auf dieser Seite
Infotext ([18/19] Mechanik - Flächenbelastung und Druck in Flüssigkeiten)
 Dieser Text basiert auf dem Artikel Druck (Physik) aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf dem Artikel Druck (Physik) aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Infotext ([20] Mechanik - Reibung)
 Dieser Text basiert auf dem Artikel Reibung aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und auf der
Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf dem Artikel Reibung aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und auf der
Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Infotext ([21] Mechanik - Drehmoment und Hebel)
 Dieser Text basiert auf dem Artikel Hebel (Physik) aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf dem Artikel Hebel (Physik) aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Infotext ([23] Mechanik - Die Arbeit )
 Dieser Text basiert auf dem Artikel Arbeit (Physik) aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf dem Artikel Arbeit (Physik) aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Infotext ([24] Mechanik - Golgene Regel der Mechanik)
 Dieser Text basiert auf dem Artikel Goldene Regel der Mechanik
aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons
CC-BY-SA 3.0 Unported (Kurzfassung). Der Text wurde von Andreas
Rueff überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf dem Artikel Goldene Regel der Mechanik
aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons
CC-BY-SA 3.0 Unported (Kurzfassung). Der Text wurde von Andreas
Rueff überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Infotext ([25] Mechanik - Die Energie)
 Dieser Text basiert auf dem Artikel Energie aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und auf der
Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf dem Artikel Energie aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und auf der
Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Infotext 1 ([26] Mechanik - Mechanische Leistung)
 Dieser Text basiert auf dem Artikel Leistung (Physik)t aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf dem Artikel Leistung (Physik)t aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Infotext 2 ([26] Mechanik - James Watt)
 Dieser Text basiert auf dem Artikel James Watt aus der freien Enzyklopädie
Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported
(Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und
auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf dem Artikel James Watt aus der freien Enzyklopädie
Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported
(Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und
auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Using PhET Simulations in Teaching
-
Simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0 (https://phet.colorado.edu).
Hintergrundbilder: Wechselbild
1) Eigenes Bild von Dr. A. Rueff
2) Das Bild von Hans Keim auf
Pixabay wurde als ein Bestandteil des zweiten
Hintergrundbildes aufgenommen (sailing-ship-4435184.jpg , Bearbeitet von Dr. A. Rueff)