Mathematik - Grundlagen für die Mittelstufe

Zahlensysteme (ℕ, ℚ, ℝ) [1/7] Gleichungen und Ungleichungen [2/7] Gleichungssysteme [3/7] Proportionen und Anwendungen [4/7] Funktionen [5/7] Geometrie [6/7] Statistik & Wahrscheinlichkeit [7/7] Fit für die Oberstufe Regelheft Analysis Analytische Geometrie Stochastik Tools

Analytische Geometrie (2)

Inhalt - Analytische Geometrie

(Vektorgeometrie)

→ Teil 1:

Einstieg / Wiederholung
Gleichungssysteme
Rechnerische Lösungsverfahren

Analytik
Koordinatensysteme
Vektoren
Vektoren addieren und subtrahieren
Das Skalarprodukt
Das Vektorprodukt (Kreuzprodukt)
Vektoren
Geradengleichung im Raum
Lagebeziehung: Punkt-Gerade
Lagebeziehung: Gerade-Gerade

Teil 2:

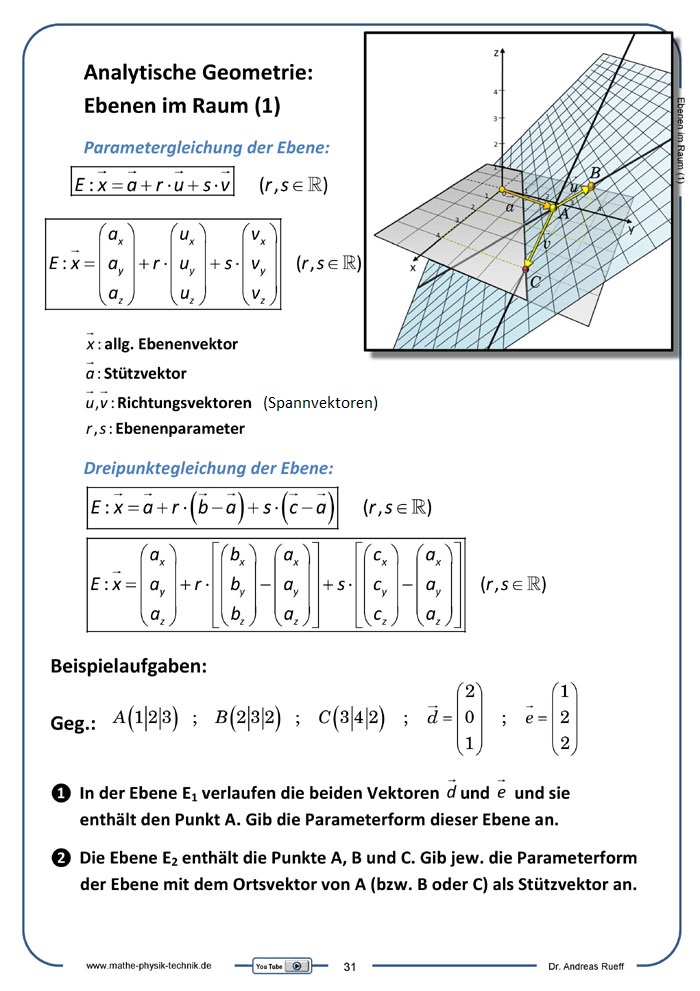
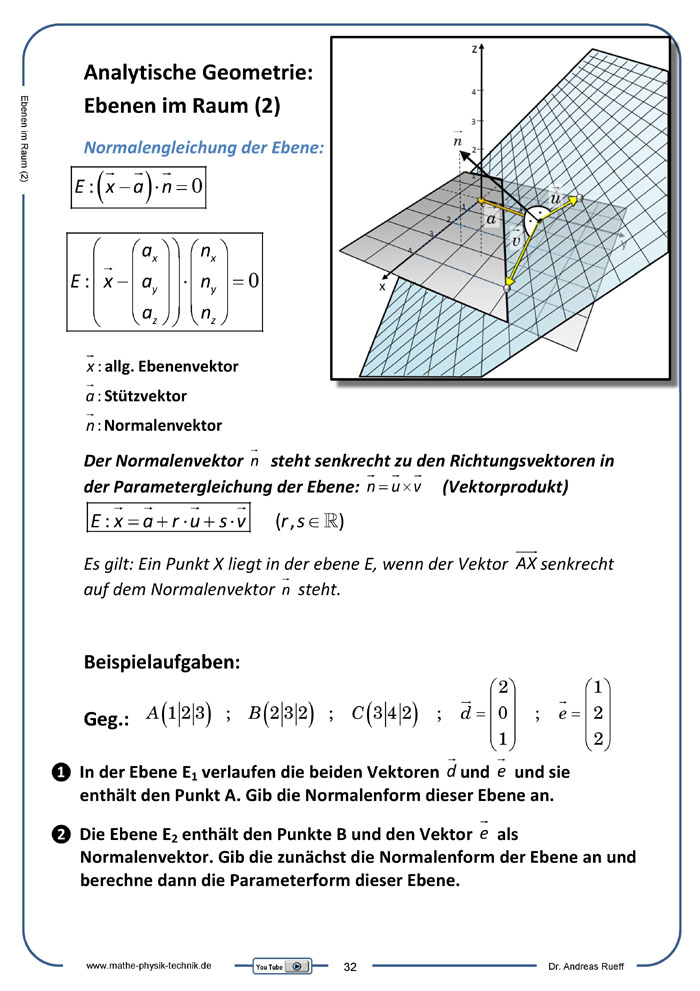
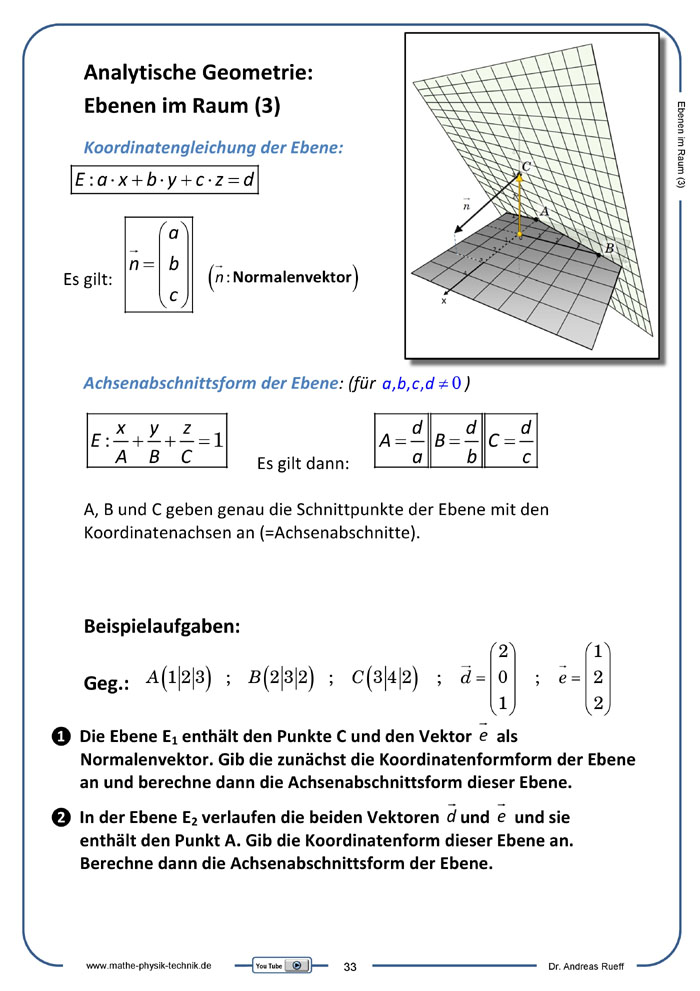
Ebenen im Raum
Parametergleichung der Ebene
Dreipunktegleichung der Ebene
Normalengleichung der Ebene
Koordinatengleichung der Ebene
Achsenabschnittsform der Ebene
Umwandlungen der Ebenengleichungen
1) Parametergleichung → Normalengleichung
2) Normalengleichung → Koordinatengleichung
3) Koordinatengleichung → Normalengleichung
4) Normalengleichung → Parametergleichung
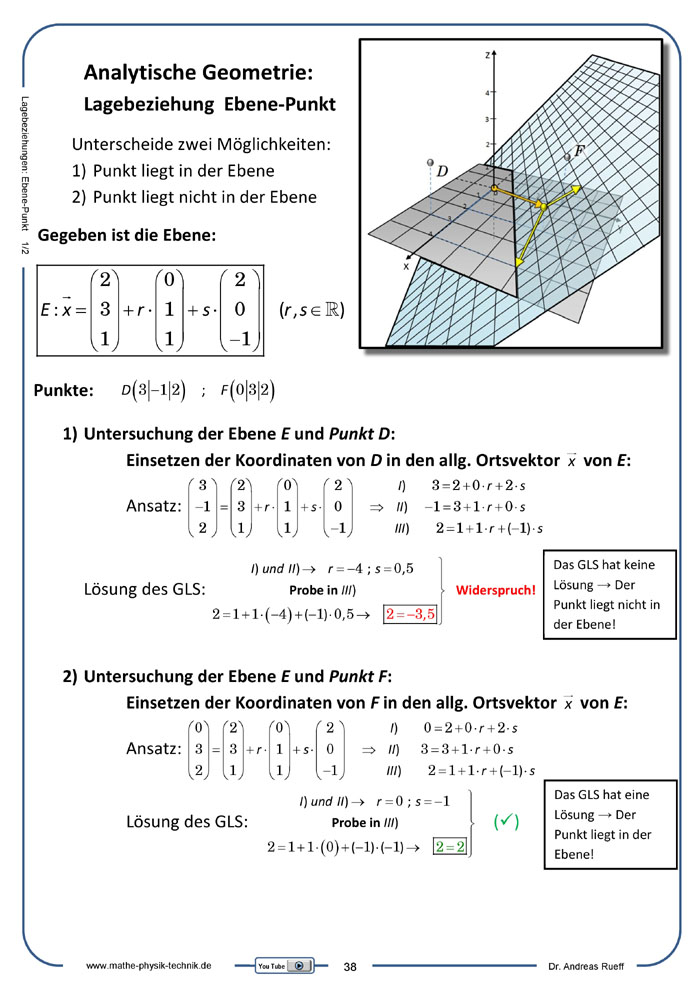
Lagebeziehung Ebene-Punkt
Lagebeziehung Ebene-Gerade
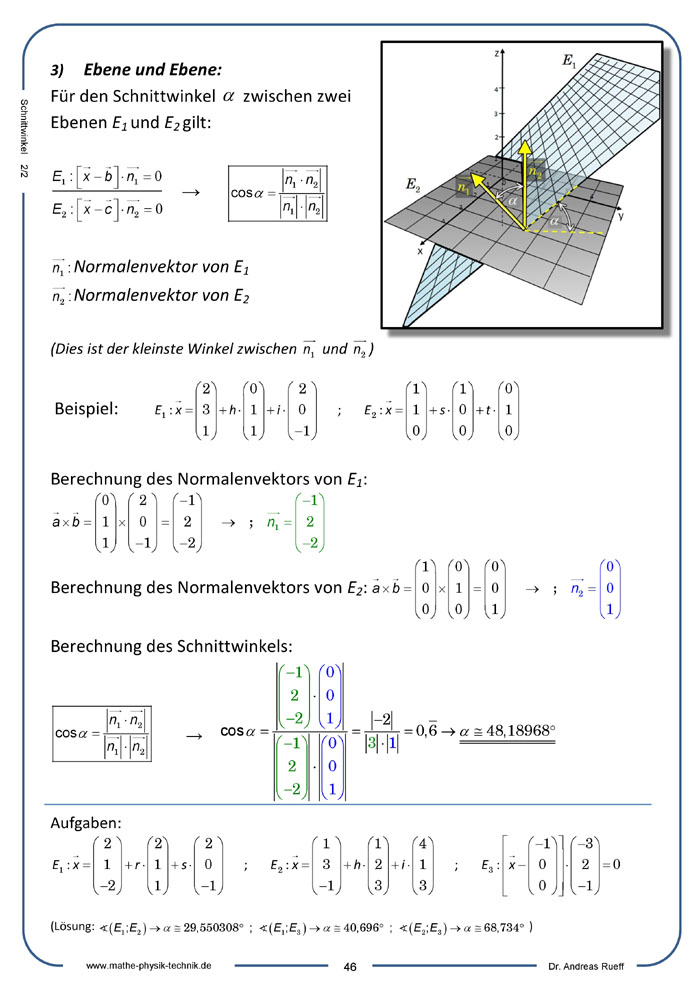
Lagebeziehung Ebene-Ebene
Schnittwinkel
Hesse’sche Normalenform der Ebene
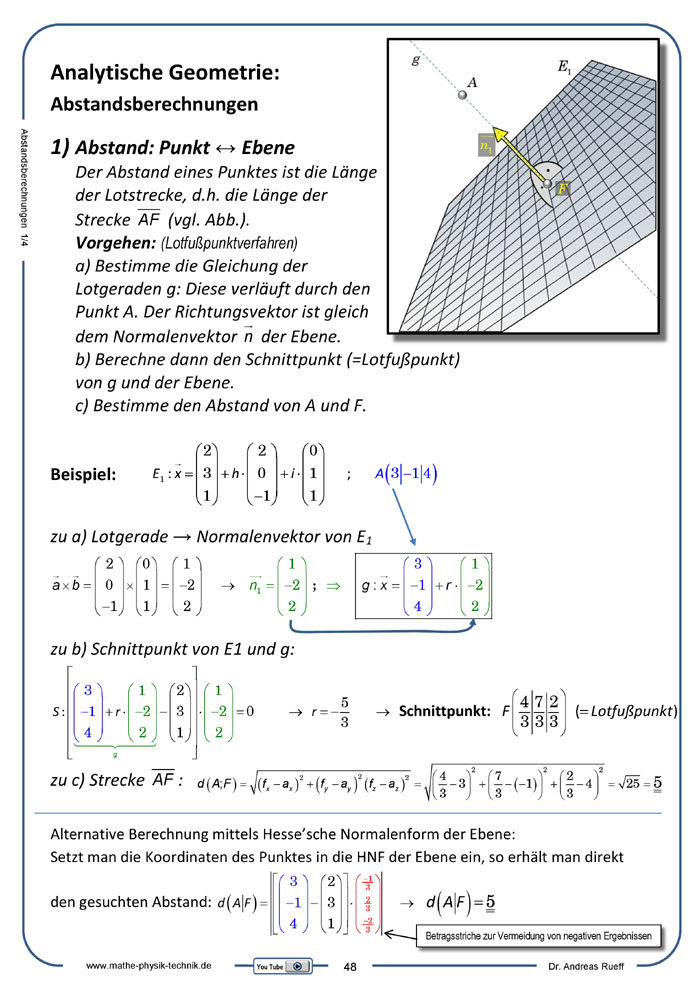
Abstandberechnungen: Punkt ↔ Ebene
Abstandberechnungen: Punkt ↔ Gerade
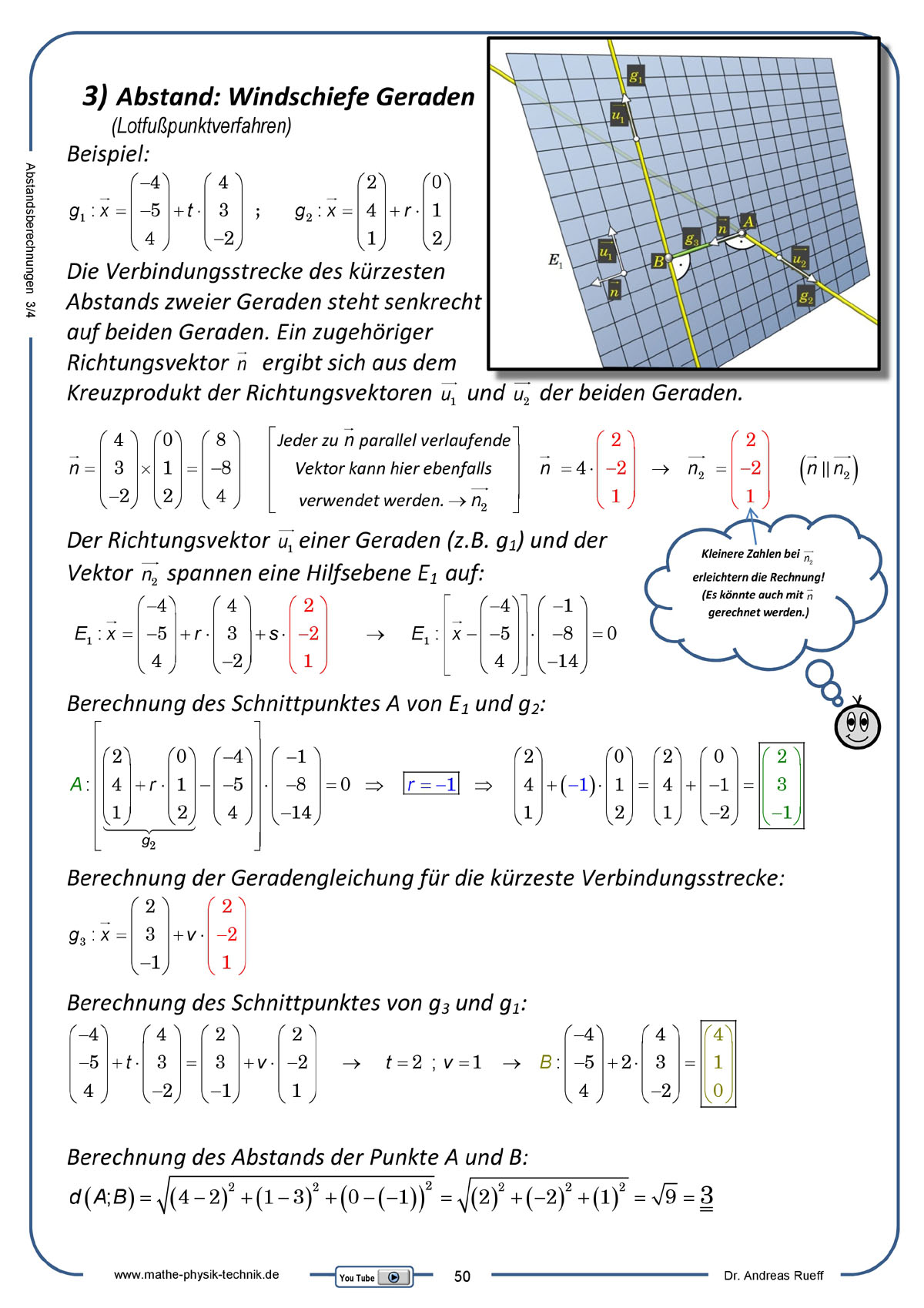
Abstandberechnungen: Gerade ↔ Gerade (Windschiefe Geraden)
Aufgaben - Abstandsberechnungen

Allgemeine Hinweise zu den Themenseiten

Die hier angebotenen Themenseiten fassen die grundlegenden Inhalte, Informationen und Hefteinträge zu den Unterrichtsinhalten von verschiedenen Themenbereichen der Fächer Mathematik, Physik und dem Wahlpflichtfach MINT/Technik zusammen. Diese sind online, kostenlos und ohne Registrierung verfügbar und sollen zur besseren Selbstorganisation der Schüler beitragen.

Die im Internet bereitgestellten Materialien bieten aber auch noch zusätzliche Möglichkeiten: Sie sollen den Schülern einen Leitfaden zur Vorbereitung auf Kursarbeiten, aber auch bei Fehlstunden zur Nacharbeit der versäumten Unterrichtsinhalte dienen und weiterhin den Eltern die Möglichkeit zur Unterstützung bei den unterrichtsbegleitenden Hilfestellungen geben. Die Zusammenfassungen zu den Unterrichtsinhalten auf den Themenseiten werden dabei jeweils ergänzt durch Lernvideos, Infotexten, Aufgaben, Bildergalerien und interaktiven Tools. Diese sollen dabei helfen selbstständig eigene Ergebnisse zu überprüfen oder zusätzliche Informationen zu den Inhalten erhalten. Bei den Lernvideos handelt es sich teilweise um die YouTube-Video des YT-Kanals Mathe-Physik-Technik. Weiterhin sind bei den einzelnen Folien zusätzliche Videovorschläge von anderen YouTube-Kanälen zugeordnet. Der jeweilige Link leitet dann ggf. direkt auf die YouTube-Video-Seite weiter.

Bei den klassischen physikalischen Themenbereichen sind die jeweiligen Folien für den digitalen Unterricht weitestgehend angepasst und optimiert worden. Insbesondere durch die Corona-Krise rückt der digitale und eigenverantwortliche Unterricht immer mehr in den Fokus. Zu den einzelnen Folien sind deshalb jeweils passende Videos zu den Inhalten zugeordnet und zu vielen Folien auch passende Aufgaben eingearbeitet worden. Dadurch sind die Themenbereiche in Teilabschnitten strukturiert und für die Arbeit mit Wochenplänen optimiert worden. Sie ermöglichen den Schülern so die selbstständige Arbeit daheim und geben jedem Schüler die Möglichkeit die Lernziele auch unter den gegebenen Umständen bestmöglich zu erreichen. Dabei können Schüler dann sogar die positiven Seiten des digitalen Unterrichts (Eigenes Lerntempo festlegen, optimale Anpassung von Lernzeit und Zeitpunkt an den eigenen Biorhythmus zum effizienten Lernen, etc.) für sich besonders gut nutzen.

Siehe hierzu auch: → Konzept - mathe-physik-technik.de

Skript → Publikationen

Hinweis:
Für die Unterrichtseinheit ist die Anschaffung des Skripts für meine Schüler nicht notwendig! Die Folien werden nacheinander bearbeitet und notwendige Materialien ggf. kopiert.

Skripte

→ Publikationen

Diese App ist eingebunden unter Verwendung von Geogebra [GNU General Public License (version 3 or later)].

[Bild kann nicht geladen werden]

Ebenen im Raum

Analytische Geometrie (Video 10): [5:47]
Ebenen im Raum (1): Ebenengleichungen

Beschrieben und anschaulich dargestellt wird die Darstellung von Ebenen im Raum. (Parameterform und Dreipunkteform der Ebene)

Diese App ist wurde erstellt von Cornelia Schmidt bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App ist wurde erstellt von A. Rueff nach einer Vorlage von Cornelia Schmidt bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

[Bild kann nicht geladen werden]

[Bild kann nicht geladen werden]

Analytische Geometrie (Video 11): [6:42]
Ebenen im Raum (2): Ebenengleichungen (Normalengleichung)

Beschrieben und anschaulich dargestellt wird im zweiten Teil zu den Ebenengleichungen die Darstellung von Ebenen im Raum durch die Normalform der Ebenengleichung.

Diese App ist wurde erstellt von A. Rueff nach einer App-Vorlage von Cornelia Schmidt bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

[Bild kann nicht geladen werden]

Analytische Geometrie (Video 12): [7:17]
Ebenen im Raum (3): Koordinatengleichung und Achsenabschnitts-

form der Ebene

Beschrieben und anschaulich dargestellt an einem Beispiel wird im dritten Teil zu den Ebenengleichungen die Darstellung von Ebenen im Raum durch die Koordinatenform der Ebenengleichung. Als Spezialfall wird die Achsenabschnittsform ebenfalls veranschaulicht.

Diese App ist wurde erstellt von A. Rueff nach einer App-Vorlage von Cornelia Schmidt bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Hinweis: Anstelle der Variablen "x" , "y" , "z" wird oft auch"x₁" , "x₂" , "x₃" geschrieben. Dies ist bei der App hier der Fall.

Diese App ist wurde erstellt von vmaier bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

[Bild kann nicht geladen werden]

Diese App ist wurde erstellt von elkeblanck bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

[Bild kann nicht geladen werden]

Lagebeziehungen

Analytische Geometrie (Video 12b): [6:08]
Lagebeziehungen: Ebene und Punkt

Beschrieben und anschaulich demonstriert werden die möglichen Lagebeziehungen eines Punktes zu einer Ebene. Die rechnerische Untersuchung wird an einem Beispiel vorgeführt.

Diese App ist wurde erstellt von A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

[Bild kann nicht geladen werden]

Analytische Geometrie (Video 12c): [6:54]
Lagebeziehungen: Ebene und Gerade mit Schnittpunktsberechnung

Beschrieben und anschaulich demonstriert werden die möglichen Lagebeziehungen einer Gerade zu einer Ebene. Die rechnerische Untersuchung des Schnittpunktes wird an einem Beispiel vorgeführt.

Diese App ist wurde erstellt von A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

[Bild kann nicht geladen werden]

Analytische Geometrie (Video 13): [5:29]
Aus zwei Ebenen (Parameterform und Normalenform) wird die Schnittgerade berechnet und veranschaulicht.

Analytische Geometrie (Video 14): [4:49]
Aus zwei Ebenen (Parameterform und Koordinatenform) wird die Schnittgerade berechnet und veranschaulicht.

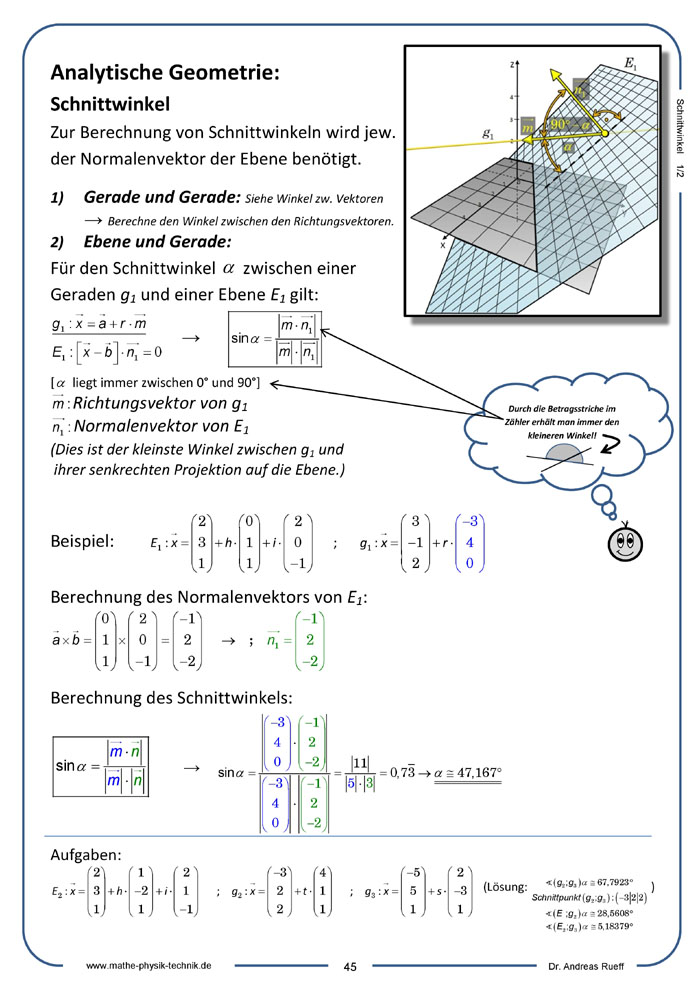
Analytische Geometrie (Video 15): [5:30]
Anschaulich vorgeführt wird die Berechnung des Abstands eines Punktes im Raum (R³) zu einer Ebene durch das Lotfußpunktverfahren.

[Bild kann nicht geladen werden]

Analytische Geometrie (Video 16): [3:49]
Anschaulich beschrieben und vorgerechnet wird ein Beispiel zur Abstandsberechnung eines Punktes zu einer Geraden im Raum (R^3) nach dem Lotfußpunktverfahren.

Analytische Geometrie (Video 17): [4:57]
Anschaulich beschrieben und vorgerechnet wird ein Beispiel zur Abstandsberechnung zweier windschiefer Geraden im Raum (R³) nach dem Lotfußpunktverfahren.

← Analytische Geometrie (1)

Alle von mir erstellten Materialien stehen für Bildungszwecke frei zur Verfügung, dürfen allerdings nicht von jemand anderem kommerziell vertrieben werden.

Erfahrungsbericht zu den Materialien:

Als geeignete Materialien haben sich u. a. die folgenden Taschenrechner erwiesen:

1) Für die Mittelstufe vollkommen ausreichend und weniger kompliziert in der

Handhabung: TI-30

2) Für die Oberstufe mit allen notwendigen Funktionen: Casio FX-991DE Plus (Dieser TR kann beispielsweise auch Integralrechnung, Vektorrechnung, Gleichungssysteme lösen, Statistik u.v.m.)

Hier einige Links die dich auch interessieren könnten:

Welt der Physik

Ziel ist es, das für viele Menschen abstrakte Thema Physik anfassbar zu machen und das Interesse Jugendlicher und Erwachsener für diesen faszinierenden Bereich der Naturwissenschaften zu wecken.

Planet Schule
Planet Schule bietet Schulfernsehsendungen zum Ansehen und Herunterladen so wie weitere Lernangebote für Lehrer, Schüler und natürlich alle Bildungsinteressierten.

→ Rückmeldung geben