Die Sonnenuhr (2)
Hinweis: Auf dieser Seite befinden sich mehrere interaktive Geo-Gebra-Simulationen.
Das Laden der Seite benötigt deshalb etwas mehr Zeit.
Hinweise zur Berechnung der Sonnenuhr
Die Berechnung der Sonnenuhr lässt sich auf einfache grundsätzliche Überlegungen zurückführen die hier im Folgenden kurz dargestellt werden.
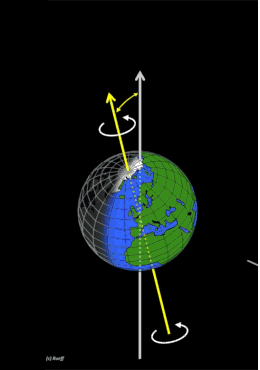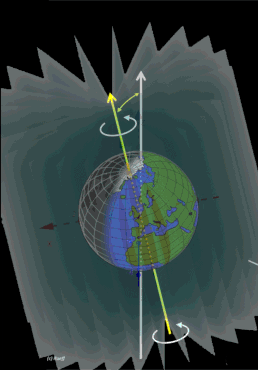
Ausgangspunkt der Überlegungen ist die Position und die Drehung der Erde bezüglich der Sonne im Weltall.
1) Festlegung des mathematischen Koordinatensystems
Für die Berechnung der vertikalen Sonnenuhr legen wir zunächst ein geeignetes Koordinatensystem fest. Hierbei wird ein dreidimensionales Koordinatensystem mit x-, y- und z-Achse für die mathematische Beschreibung verwendet, mit Hilfe der analytischen Geometrie werden die weiteren Berechnungen durchgeführt.
2) Stundenebenen
Die Erde dreht sich an einem Tag einmal um die eigene Achse. Dabei spannt die Erdachse mit der Sonne als weiteren Punkt im Raum eine Ebene auf. Bei 24 Stunden für eine volle Umdrehung bedeutet das, dass sich für jede Stunde eine Ebene im Raum ergibt. Diese unterscheiden sich voneinander durch eine 15°-Rotation (360°:24=15°) um die Erdachse. Nach 12 Stunden befindet man sich dann wieder auf der ersten Ebene (aber auf der anderen Seite der Erde). Die folgenden 12 Ebenen sind dann jeweils identisch mit den ersten 12 Ebenen. Die Beschreibung reduziert sich also auf 12 Ebenen im Raum.
Zusammenfassend bedeutet das: Für den Zeitraum von 1 Uhr bis 12 Uhr ergeben sich also 12 Ebenen die alle die Erdachse beinhalten. Die jeweils nächste Stundenebene ergibt sich aus der vorherigen durch eine 15°-Rotation um die Erdachse. Die 1-Uhr-Ebene ist darüber hinaus dann identisch mit der 13-Uhr-Ebene, die 2-Uhr-Ebene ist identisch mit der 14-Uhr-Ebene usw.
3) Festlegung der Rotationsachse und Beschreibung der Stundenebenen
Zentraler Bestandteil der Sonnenuhr ist der Schattenstab (Gnomon). Zur Beschreibung der Stundenebenen soll die y-Achse des Koordinatensystems den Schattenstab der Sonnenuhr darstellen. Hierbei gilt: Der Schattenstab einer Sonnenuhr liegt immer parallel zur Erdachse. Mit hinreichender Genauigkeit kann für die Berechnung der Sonnenuhr davon ausgegangen werden, dass der Schattenstab mit der Erdachse gleichgesetzt wird. Das bedeutet, dass die y-Achse unseres Koordinatensystems jeweils Teil der Stundenebenen ist. Durch die Einteilung eines Tages in 24 Stunden ergibt sich für die Stundenebenen (grün), dass sich diese jeweils durch eine Drehung um 15° um die y-Achse ergeben. Wir erhalten dadurch die 12 Stundenebenen die in der animierten Abbildung dargestellt sind. Die interaktive Simulation (1) zeigt die Stundenebenen im mathematischen Modell.
Simulation 1: Stundenebenen, y-Achse als Schattenstab
4) Erhebungswinkel
Je nach Standort muss die Position und Ausrichtung des Schattenstabes genau bestimmt werden. Dabei gehen wir zunächst von einer Sonnenuhr aus die exakt nach Süden ausgerichtet ist. Der Schattenstab schließt dann mit Wandebene den sogenannten Schattenwinkel ein. Dieser berechnet sich durch die Differenz aus 90° und dem jeweiligen Erhebungswinkel am Standort. In unserem Beispiel befindet sich Kaiserslautern auf einer geografischen Breite von ca. 49,7° (=Erhebungswinkel). Daraus berechnet sich der Schattenwinkel dann zu 40,3°.
Wandebene (1): Im mathematischen Modell wird jetzt die Wandebene (blau) hinzugefügt. Diese ist hier zunächst exakt nach Süden ausgerichtet. Sie muss mit der y-Achse den Schattenwinkel einschließen. Die folgende Simulation (2) stellt diese Wandebene im Koordinatensystem dar.
Simulation 2: Wandebene (1), y-Achse als Schattenstab
5) Festlegung der 12-Uhr-Ebene
Zur Mittagszeit erreicht die Sonne von der Erdoberfläche aus betrachtet ihren höchsten Stand. Dieser Zeitpunkt wird als "Mittag" definiert und halbiert den Tag in zwei gleiche Hälften. Die Zeit vorher ist der "Vormittag", danach der "Nachmittag". Die entsprechende Stundenebene ist die 12-Uhr-Ebene. In unserem mathematischen Modell bedeutet das, dass der Schattenstab einen Schatten auf die Wandebene wirft der genau senkrecht zur Horizontalen verläuft. Die entsprechende Stundenebene wird im Koordinatensystem durch die y-z-Ebene beschrieben. Das ist in Simulation (3) dargestellt.
Simulation 3: Wandebene (1) mit 12-Uhr-Ebene, y-Achse als Schattenstab
6) Bestimmung der Stunden-Markierungen auf der Wandebene
Die Stunden-Markierungen auf der Wandebene ergeben sich jetzt aus den Schnittgeraden der Stundenebenen mit der Wandebene. In Simulation (4) ist stellvertretend neben der 12-Uhr-Ebene noch die 11-Uhr, die 10-Uhr und die 9-Uhr-Ebene dargestellt. Hierbei ist zu beachten, dass sich die Sonne (scheinbar) von Osten über Süden nach Westen am Himmel bewegt. Der Schatten des Schattenstabes fällt also jeweils genau in der entsprechenden Stundenebene auf die Wandebene. Der Schatten bewegt sich dabei im Gegenuhrzeigersinn. Die 11-Uhr-Markierung liegt also links neben der 12-Uhr-Markierung, usw.. Bei der exakt nach Süden ausgerichteten Sonnenuhr erhalten wir über diese Vorgehensweise ein achsensymmetrisches Bild der Stunden-Markierungen auf der Wandebene.
Simulation 4: Wandebene (1) mit vier Stundenebenen
6) Wandabweichung (Deklination)
Oft ist die Wand an der sich die Sonnenuhr befindet sich exakt nach Süden ausgerichtet. Hier muss dann die sogenannte Wandabweichung (Deklination) berücksichtigt werden. In unserem Beispiel hier bei der Sonnenuhr ist die Wandabweichung sehr groß, sie beträgt -51°. Das bedeutet, dass ein senkrecht auf der Wand stehende Stab um 51° mit der Südrichtung einen Winkel von 51° einschließt. Die Drehung um 51° erfolgt dabei horizontal in Richtung Süd-Osten (Wandabweichungen in Richtung Süd-Westen werden mit positiven Werten für den Deklinationswinkel angegeben.). Das bedeutet, von oben betrachtet erfolgt die Drehung im Gegenuhrzeigersinn. Die Wandabweichung führt dazu, dass die Sonnenuhr nicht mehr symmetrisch zur 12-Uhr-Markierung ist. Hier im Beispiel sieht man auch, dass durch die Deklination ab Nachmittag die Sonne nicht mehr auf die Sonnenuhr scheint und entsprechend keine Markierungen mehr vorhanden sind. In solchen Fällen wird dann ggf. eine zweite Sonnenuhr mit positiver Deklination an einer anderen Wand angebracht für die Nachmittags- und Abendstunden.
In der Simulation (5) ist die Wandebene (2) mit der Wandabweichung gelb eingetragen, sie ergibt sich aus der blauen Wandebene (1) durch eine Rotation um die Schnittgerade der blauen Wandebene mit der 12-Uhr-Ebene.
Simulation 5: Wandebene (2) mit 12-Uhr-Ebene und Wandebene (1)
7) Stundenmarkierungen
Die Markierungen für die Sonnenuhr ergeben sich auch jetzt wieder durch die Schnittgeraden der Wandebene (2) mit den Stundenebenen. In Simulation (6) sind stellvertretend sechs Stundenebenen und die Wandebene (2) eingetragen.
Simulation 6: Wandebene (2) mit sechs Stundenebenen
In Simulation (7) sind die so berechneten Schnittgeraden auf der Wandebene (2) eingetragen (die Stundenebenen sind hier ausgeblendet). Die 12-Uhr-Markierung ist grün dargestellt und muss bei der Sonnenuhr vertikal orientiert sein. Zusätzlich ist hier eine blaue Horizontale mit eingetragen (verläuft senkrecht zur 12-Uhr-Markierung) und rot die Begrenzungen der Sonnenuhr, so wie sie an der Wand angebracht werden kann.
Simulation 7: Wandebene (2) mit Stundenmarkierungen und Hilfslinien
8) Befestigung des Schattenstabes
Mit Hilfe der mathematischen Simulation lassen sich jetzt auch geeignete Befestigungspunkte für den Schattenstab und zwei Stützstäbe bestimmen. In Simulation (8) sind die ermittelten Strecken orange eingetragen worden.
Simulation 8: Schattenstab mit Stützstäben und Hilfslinien
Mehr Infos (planet-wissen.de):
Weitere Informationen zum Thema "Sommerzeit" gibt es hier:
Alle von mir erstellten Materialien stehen für Bildungszwecke frei zur Verfügung, dürfen allerdings nicht von jemand anderem kommerziell vertrieben werden.
Quellenangaben zu den Inhalten auf dieser Seite
Bildergalerie zur Sonnenuhr in Kaiserslautern
Bildquelle-Zeitzonenkarten (Vorlage): By Ssolbergj [GFDL, CC BY-SA 3.0 or GFDL], via Wikimedia Commons | Nachbearbeitung: Rueff
.png){kind=link}
Hintergrundbild: Eigenes Bild (Dr. A. Rueff)